题目内容
17.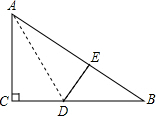 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,将纸片沿AD折叠,直角边AC恰好落在斜边上,且与AE重合,则△BDE的面积为6cm2.
如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,将纸片沿AD折叠,直角边AC恰好落在斜边上,且与AE重合,则△BDE的面积为6cm2.
分析 先根据勾股定理求得AB的长,再根据折叠的性质求得AE,BE的长,从而利用勾股定理可求得DE的长,于是得到结论.
解答 解:∵AC=6cm,BC=8cm,
∴AB=10cm,
∵AE=6cm(折叠的性质),
∴BE=4cm,
设CD=DE=x,则在Rt△DEB中,42+x2=(8-x)2,
解得x=3,
即DE等于3cm.
∴△BDE的面积=$\frac{1}{2}$×4×3=6,
故答案为:6,
点评 本题考查了翻折变换(折叠问题),以及利用勾股定理解直角三角形的能力,即:直角三角形两直角边的平方和等于斜边的平方.

练习册系列答案
相关题目
2.已知|x|=2,|y|=4,且x>y,则x-y的值为( )
| A. | 6 | B. | 6或2 | C. | ±6或±2 | D. | -2或-6 |
 如图,已知∠B=∠E,AB=DE,要推得△ABC≌△EDF,若以“AAS”为依据,缺条件∠ACB=∠DFE.
如图,已知∠B=∠E,AB=DE,要推得△ABC≌△EDF,若以“AAS”为依据,缺条件∠ACB=∠DFE.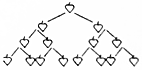 如图是一副“苹果图”,第一行有1个苹果,第二行有2个苹果,第三行有4个苹果,第四行有8个苹果…,猜猜第十行有29个苹果,第2017行有22016个苹果.
如图是一副“苹果图”,第一行有1个苹果,第二行有2个苹果,第三行有4个苹果,第四行有8个苹果…,猜猜第十行有29个苹果,第2017行有22016个苹果.