Question

【题目】如图，抛物线经过、两点，与轴交于另一点．

求此抛物线的解析式；

已知点在第四象限的抛物线上，求点关于直线对称的点的坐标．

在的条件下，连接，问在轴上是否存在点，使？若存在，请求出点的坐标；若不存在，请说明理由．

Answer 1

【答案】 ；点关于直线对称的点；存在．，或．

【解析】

（1）将A（-1，0）、C（0，-3）两点坐标代入抛物线y=ax2+bx-3a中，列方程组求a、b的值即可；

（2）将点D（m，-m-1）代入（1）中的抛物线解析式，求m的值，再根据对称性求点D关于直线BC对称的点D'的坐标；

（3）分两种情形①过点C作CP∥BD，交x轴于P，则∠PCB=∠CBD，②连接BD′，过点C作CP′∥BD′，交x轴于P′，

分别求出直线CP和直线CP′的解析式即可解决问题．

将、代入抛物线中，

得，

解得，

∴；

将点代入中，得

，

解得或，

∵点在第四象限，

∴，

∵直线解析式为，

∴，，，

∴点关于直线对称的点；

存在．

过点作轴，垂足为，交直线于点（如图），

∵，

∴，

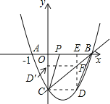
又∵轴，四边形为平行四边形，

∴，

∴，

设与相交于点，

易求解析式为：，

由，得到关于的方程，解方程后，得；

于是，点坐标为：；

于是解析式为：，

令方程中，，则，

所以，点坐标为：，

∴，或．