题目内容
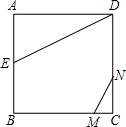 如图,正方形ABCD的边长为2
如图,正方形ABCD的边长为2| 5 |
| 5 |
考点:相似三角形的判定
专题:
分析:根据题意不难确定Rt△AED的两直角边AD=2AE.再根据相似的性质及变化,可考虑Rt△MCN的两直角边MC、NC间的关系满足是
或2倍.求得CM的长.
| 1 |
| 2 |
解答:解:如图,正方形ABCD的边长为2
,E为AB中点,
∴AE=
AD=
.
设CM的长为x.
在Rt△MNC中
∵MN=
,
∴NC=
,
①当Rt△AED∽Rt△CMN时,
则
=
,
即
=
,
解得x=1或x=-1(不合题意,舍去),
②当Rt△AED∽Rt△CNM时,
则
=
,即
=
,
解得x=2或-2(不合题意,舍去),
综上所述,当CM=1或2时,△AED与以M,N,C为顶点的三角形相似.
故答案为:1或2.
| 5 |
∴AE=
| 1 |
| 2 |
| 5 |
设CM的长为x.
在Rt△MNC中
∵MN=
| 5 |
∴NC=
| 5-x2 |
①当Rt△AED∽Rt△CMN时,
则
| AE |
| CM |
| AD |
| CN |
即
| ||
| x |
2
| ||
|
解得x=1或x=-1(不合题意,舍去),
②当Rt△AED∽Rt△CNM时,
则
| AE |
| CN |
| AD |
| CM |
| ||
|
2
| ||
| x |
解得x=2或-2(不合题意,舍去),
综上所述,当CM=1或2时,△AED与以M,N,C为顶点的三角形相似.
故答案为:1或2.
点评:本题考查相似三角形的判定与性质、正方形的性质.解决本题特别要考虑到①当Rt△AED∽Rt△CMN时②当Rt△AED∽Rt△CNM时这两种情况.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

