题目内容
(8分)如图,过点B的直线l: 交y轴于点A,与反比例函数
交y轴于点A,与反比例函数 的图象交于点C(2,n)和点D.
的图象交于点C(2,n)和点D.


(1)求m和n的值,及另一交点D的坐标;
(2)求△COD的面积。
(1) m=-4,n=-2 D(-1,4) (2) 3
解析试题分析:解:∵直线l与反比例相交于C、D,且C(2,n)
∴-2×2+2=n,即n=-2
∴C(2,-2)
∴m="x" y=-2×2=-4
由y=-2x+2和y=- 得
得
x1=2,y1=-2或x2=-1,y2=4
又C(2,-2),所以D(-1,4)
(2)令y=-2x+2得x=OB=1
S△COD=S△OBD+S△OBC
= ·OB·y D+
·OB·y D+ ·OB·y C
·OB·y C
= ×1×4+
×1×4+ ×1×2
×1×2
=3
考点:一次函数与反比例函数组合考察
点评:根据已知条件,画出相关函数图像,观察点与函数的关系,利用函数求出点的坐标,通过点的坐标求出函数,结合图像是解决问题的捷径。

练习册系列答案
相关题目
 如图,过点O的直线与双曲线y=
如图,过点O的直线与双曲线y=| k |
| x |
| A、S1=S2 |
| B、2S1=S2 |
| C、3S1=S2 |
| D、无法确定 |
 截直线l所得线段CD=
截直线l所得线段CD=

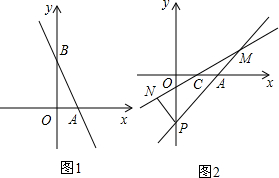 如图1,在平面直角坐标系中,A(a,0),B(0,b),且a,b满足b=
如图1,在平面直角坐标系中,A(a,0),B(0,b),且a,b满足b=