题目内容
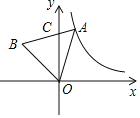
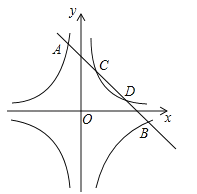
【题目】如图，直线y=-x+b与双曲线
分别相交于点A，B，C，D，已知点A的坐标为（-1，4），且AB：CD=5：2，则m=_________．
【答案】
【解析】
如图由题意：k＝﹣4，设直线AB交x轴于F，交y轴于E．根据反比例函数y
和直线AB组成的图形关于直线y＝x对称，求出E、F、C、D的坐标即可．
如图由题意：k＝﹣4，设直线AB交x轴于F，交y轴于E．
∵反比例函数y和直线AB组成的图形关于直线y＝x对称，A（﹣1，4），∴B（4，﹣1），∴直线AB的解析式为y＝﹣x+3，∴E（0，3），F（3，0），∴AB＝5
，EF＝3．
∵AB：CD＝5：2，∴CD＝2，∴CE＝DF
．设C（x，－x+3），∴CE=
，解得：x=
（负数舍去），∴x=
，－x+3=
，∴C（
），∴m=
=．
故答案为：．
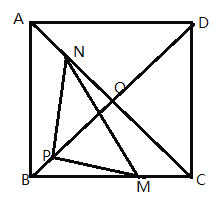
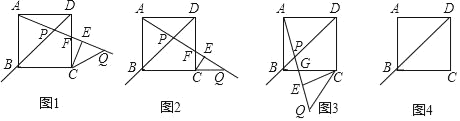
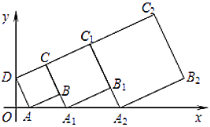
【题目】在平面坐标系中，正方形
的位置如图所示，点
的坐标为
，点
的坐标为
，延长
交
轴于点
，作正方形
，正方形的面积为______，延长
交轴于点
，作正方形
，……按这样的规律进行下去，正方形
的面积为______.
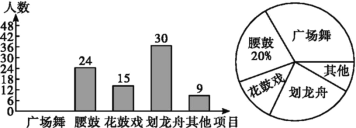
【题目】某区在实施居民用水管理前，随机调查了部分家庭（单位：户）去年的月均用水量（单位：t），并将调查数据进行整理，绘制出如下不完整的统计图表：
月均用水量 | 频数 | 频率 |
0≤x＜5 | 6 | 12% |
5≤x＜10 | 12 | 24% |
10≤x＜15 |
| 32% |
15≤x＜20 | 10 | 20% |
20≤x＜25 | 4 |
|
25≤x＜30 | 2 | 4% |
合计 |
| 100% |
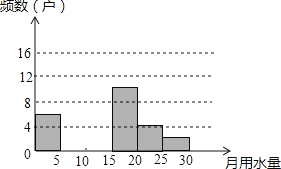
请解答以下问题：
（I）把上面的频数分布表和频数分布直方图补充完整；
（Ⅱ）若该小区有2000户家庭，根据此次随机抽查的数据估计，该小区月均用水量不低于20t的家庭有多少户？
（Ⅲ）为了鼓励节约用水，要确定一个月均用水量的标准，超出该标准的部分按1.5倍价格收费，若要使68%的家庭水费支出不受影响，那么，你觉得家庭月均用水量应定为多少？
