��Ŀ����
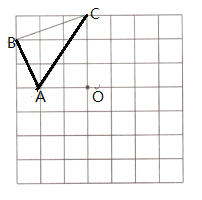
����Ŀ�����꼶��ѧѧϰ����С����ѧ����ͼ�ε����ơ���һ�º��ֿɽ����������εĶ��塢�ж��Լ�������չ�����Ρ����ε�������ȥ���磺���ǿ��Զ��壺�����Ϳ�֮����ȵľ��������ƾ��Σ������ƾ���Ҳ�����µ����ʣ����ƾ��εĶԽ���֮�ȵ������Ʊȣ��ܳ��ȵ������Ʊȣ�����ȵ������Ʊȵ�ƽ���ȵȣ�����������ѧϰС�飬һͬ̽���������⣺
![]() д���ж��������Ƶ�һ���ж�����������һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ����������������������ƣ�
д���ж��������Ƶ�һ���ж�����������һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ����������������������ƣ�
![]() ��ͼ��������
��ͼ��������![]() ����ֱ��
����ֱ��![]() ����ƽ�ƺ�õ�����
����ƽ�ƺ�õ�����![]() ����֤�����ı���
����֤�����ı���![]() �����Σ�������
������������![]() ����
����![]() ��
��
![]() ��
��![]() ������
������![]() �����������
�����������![]() �����һ�룬��ƽ�Ƶľ���
�����һ�룬��ƽ�Ƶľ���![]() �ij���
�ij���
���𰸡�![]() ��һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ�������
��һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ�������![]() ֤����������
֤����������![]() ��
��
��������
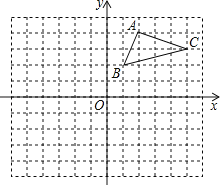
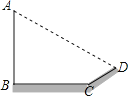
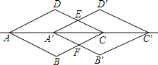
��1�������ı���ȣ�����һ���Ӧ����ȼ��ɣ���2���ɣ�1���Ľ��ۣ�������֪������DAB����D��A��B����֤�����ƣ���3����������ȵ������Ʊȵ�ƽ����A��C��������AA��.
![]() ��һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ�������
��һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ�������
![]() ����
����![]() ��
��![]() ����
����![]()
������![]() �Ľ��ۣ��õ�֤����
�Ľ��ۣ��õ�֤����
![]() ������
������![]() ����
����![]() ������
������![]() �����������
�����������![]() �����һ�룬
�����һ�룬
������![]() ������
������![]() �������Ϊ
�������Ϊ![]() ��
��
����Ӧ��֮��Ϊ![]() ����
����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��

����Ŀ��ij��Ϊ֧Ԯ�������裬�ƻ���![]() ��
��![]() �����ֵ����ͼ������ʷֱ�Ϊ60�ֺ�140�֣����мס��������м������ʷֱ�Ϊ120�ֺ�80�֣���֪�ס��������˵�
�����ֵ����ͼ������ʷֱ�Ϊ60�ֺ�140�֣����мס��������м������ʷֱ�Ϊ120�ֺ�80�֣���֪�ס��������˵�![]() ��
��![]() ���ص�ÿ�����ʵ��˷������ʾ��
���ص�ÿ�����ʵ��˷������ʾ��
�� | �� | |
| 20Ԫ/�� | 15Ԫ/�� |
| 25Ԫ/�� | 24Ԫ/�� |
��1������˵�![]() �صļ�������Ϊ
�صļ�������Ϊ![]() �֣������˷�
�֣������˷�![]() ��Ԫ������
��Ԫ������![]() ���֣��ĺ�����ϵʽ����д��
���֣��ĺ�����ϵʽ����д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����������˷ѣ���˵�����˷����ʱ�����ͷ�����