题目内容
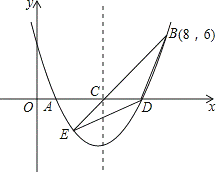
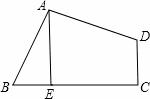
如图,二次函数y= x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点.连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.
(4)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP= S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
(1)二次函数解析式为:y= x2﹣4x+6;
x2﹣4x+6;
(2)函数图象的顶点坐标为(4,﹣2),点D的坐标为(6,0);
(3)△BDE的面积为7.5.
(4)存在,P1(4+ ,
,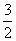 ),P2(4﹣
),P2(4﹣ ,
,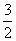 ),P3(3,﹣
),P3(3,﹣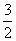 ),P4(5,﹣
),P4(5,﹣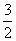 ).
).
【解析】(1)∵二次函数y= x2+bx+c的图象过A(2,0),B(8,6)
x2+bx+c的图象过A(2,0),B(8,6)
∴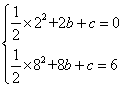 ,解得
,解得 ,∴二次函数解析式为:y=
,∴二次函数解析式为:y= x2﹣4x+6;
x2﹣4x+6;
(2)由y= x2﹣4x+6,得y=
x2﹣4x+6,得y= (x﹣4)2﹣2,∴函数图象的顶点坐标为(4,﹣2),
(x﹣4)2﹣2,∴函数图象的顶点坐标为(4,﹣2),
∵点A,D是y= x2+bx+c与x轴的两个交点,又∵点A(2,0),对称轴为x=4,
x2+bx+c与x轴的两个交点,又∵点A(2,0),对称轴为x=4,
∴点D的坐标为(6,0);
(3)∵二次函数的对称轴交x轴于C点.∴C点的坐标为(4,0)∵B(8,6),
设BC所在的直线解析式为y=kx+b,∴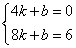 解得
解得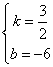
∴BC所在的直线解析式为y=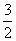 x﹣6,∵E点是y=
x﹣6,∵E点是y=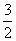 x﹣6与y=
x﹣6与y= x2﹣4x+6的交点,∴
x2﹣4x+6的交点,∴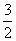 x﹣6=
x﹣6= x2﹣4x+6,解得x1=3,x2=8(舍去),当x=3时,y=﹣3,∴E(3,﹣
x2﹣4x+6,解得x1=3,x2=8(舍去),当x=3时,y=﹣3,∴E(3,﹣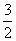 ),
),
∴△BDE的面积=△CDB的面积+△CDE的面积= ×2×6+
×2×6+ ×2×
×2×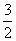 =7.5.
=7.5.
(4)存在,
设点P到x轴的距离为h,
∵S△BCD= ×2×6=6,S△ADP=
×2×6=6,S△ADP= ×4×h=2h,∵S△ADP=
×4×h=2h,∵S△ADP= S△BCD ,∴2h=6×
S△BCD ,∴2h=6× ,解得h=
,解得h=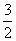 ,
,
当P在x轴上方时,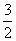 =
= x2﹣4x+6,解得x1=4+
x2﹣4x+6,解得x1=4+ ,x2=4﹣
,x2=4﹣ ,
,
当P在x轴下方时,﹣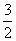 =
= x2﹣4x+6,解得x1=3,x2=5,
x2﹣4x+6,解得x1=3,x2=5,
∴P1(4+ ,
,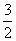 ),P2(4﹣
),P2(4﹣ ,
,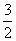 ),P3(3,﹣
),P3(3,﹣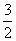 ),P4(5,﹣
),P4(5,﹣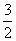 ).
).

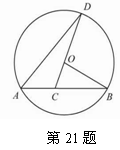


 =0,那么菱形的面积等于 .
=0,那么菱形的面积等于 .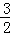 ,0),且与反比例函数y=
,0),且与反比例函数y=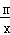 (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.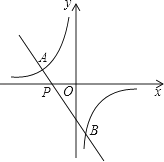
 ,则 AC=( )
,则 AC=( )
 ,不是黄球的概率是
,不是黄球的概率是 ,则mn=
,则mn=