题目内容
已知,如图1:在正方形ABCD中,AB=2,点P是DC延长线上一点,以P为圆心,PD长为半径的圆的一段弧交AB边于点E,(1)若以A为圆心,AE为半径的圆与以BC为直径的圆外切时,求AE的长;
(2)如图2:连接PE交BC边于点F,连接DE,设AE长为x,CF长为y,求y与x的函数关系式,并写出自变量x的取值范围;
(3)将点B沿直线EF翻折,使点B落在平面上的B′处,当EF=
| 5 | 3 |
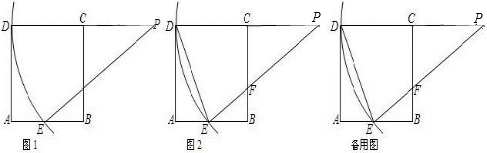
分析:(1)两圆外切,则圆心距等于两圆的半径和;设BC的中点为G,那么AG的长应该是AE+
BC,进而可在Rt△ABG中,由勾股定理求得AE的长.
(2)若要x、y发生联系,需将它们构建到同一个直角三角形中;连接DF,过D作DH⊥PE于H;通过证△DAE≌△DHE得到AE=EH=x,通过证△DHF≌△DCF得到CF=FH=y,进而可在Rt△EFB中,根据勾股定理求得x、y的函数关系式;
(3)由(2)知:当EF=
时,x+y=
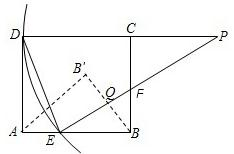
,联立(2)的函数关系式可求得此时x的值,进而可求出AE、BF的长;根据折叠的性质知:EF垂直平分BB′,设垂足为Q;在Rt△BEF中,根据直角三角形面积的不同表示方法,可求得BQ的长,也就得出了BB′的长;然后再判断两个直角三角形的对应边是否成比例即可.
| 1 |
| 2 |
(2)若要x、y发生联系,需将它们构建到同一个直角三角形中;连接DF,过D作DH⊥PE于H;通过证△DAE≌△DHE得到AE=EH=x,通过证△DHF≌△DCF得到CF=FH=y,进而可在Rt△EFB中,根据勾股定理求得x、y的函数关系式;
(3)由(2)知:当EF=
| 5 |
| 3 |
| 5 |
| 3 |
解答:解:(1)取BC的中点G,连接AG.(1分)
∵圆A与圆G圆外切,
∴AG=AE+1.(1分)
正方形ABCD中,AB=2,设AE=x.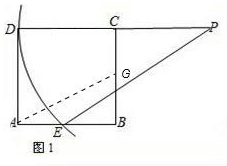
∵在Rt△ABG中,AB2+BG2=AG2,(1分)
∴22+12=(x+1)2x=±
-1(负数舍去).(1分)
∴以A为圆心,AE为半径的圆与以BC为直径的圆外切时,AE的长为
-1.
(2)过点D作DH⊥PE于H,连接DF.(1分)
∵PD=PE,
∴∠PDE=∠PED.
∵四边形ABCD为正方形,
∴DC∥AB,
∴∠PDE=∠DEA,
∴∠PED=∠DEA;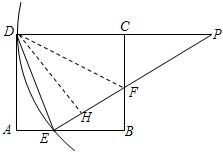
∵∠A=∠DHE=90°,DE=DE,
∴△DAE≌△DHE;
∴DA=DH,EA=EH.(1分)
∵DC=DH,∠DCF=∠DHF=90°,DF=DF,
∴△DHF≌△DCF;
∴CF=FH;(1分)
∵AE=x,CF=y,
∴EF=x+y,BE=2-x,BF=2-y;
∴在直角三角形BEF中,BE2+BF2=EF2,
∴(2-x)2+(2-y)2=(x+y)2,
整理得到:y=
(0<x<2);(2分)
(3)∵EF=
,
∴x+y=
,
∴
-x=
,
解得:x1=1,x2=
.(1分)
当x1=1时,BE=1,BF=
;
∵B沿直线EF翻折落在平面上的B'处,
∴BB'⊥EF,设垂足为Q.
∴BQ=
,BB'=
.
∵E、Q分别为AB、BB'的中点,
∴EQ∥AB',
∴∠ABB'=∠EQB=90°.
在△AB'B与△BEF中,
=
=
,
=
=
,
∴
=
,
∴△AB'B∽△BEF;(3分)
(用相似传递性也可以证明△AB'B∽△BEF,也按步骤分步得分)
当x2=
时,BE=
,BF=1.
∵
=
=2,
=1,
EQ与AB'不平行,
∴△ABB'不是直角三角形,
∴△AB'B与△BEF不相似.(1分)
综上所述,当EF=
,AE=1时,△AB'B∽△BEF;
当EF=
,AE=
时,△AB'B与△BEF不相似.
∵圆A与圆G圆外切,
∴AG=AE+1.(1分)
正方形ABCD中,AB=2,设AE=x.

∵在Rt△ABG中,AB2+BG2=AG2,(1分)
∴22+12=(x+1)2x=±
| 5 |
∴以A为圆心,AE为半径的圆与以BC为直径的圆外切时,AE的长为
| 5 |
(2)过点D作DH⊥PE于H,连接DF.(1分)
∵PD=PE,
∴∠PDE=∠PED.
∵四边形ABCD为正方形,
∴DC∥AB,
∴∠PDE=∠DEA,
∴∠PED=∠DEA;

∵∠A=∠DHE=90°,DE=DE,
∴△DAE≌△DHE;
∴DA=DH,EA=EH.(1分)
∵DC=DH,∠DCF=∠DHF=90°,DF=DF,
∴△DHF≌△DCF;
∴CF=FH;(1分)
∵AE=x,CF=y,
∴EF=x+y,BE=2-x,BF=2-y;
∴在直角三角形BEF中,BE2+BF2=EF2,
∴(2-x)2+(2-y)2=(x+y)2,
整理得到:y=
| 4-2x |
| x+2 |

(3)∵EF=
| 5 |
| 3 |
∴x+y=
| 5 |
| 3 |
∴
| 5 |
| 3 |
| 4-2x |
| x+2 |
解得:x1=1,x2=
| 2 |
| 3 |
当x1=1时,BE=1,BF=
| 2 |
| 3 |
∵B沿直线EF翻折落在平面上的B'处,
∴BB'⊥EF,设垂足为Q.
∴BQ=
| 2 |
| 5 |
| 4 |
| 5 |
∵E、Q分别为AB、BB'的中点,
∴EQ∥AB',
∴∠ABB'=∠EQB=90°.
在△AB'B与△BEF中,
| BB′ |
| AB |
| ||
| 2 |
| 2 |
| 5 |
| BF |
| EF |
| ||
|
| 2 |
| 5 |
∴
| BB′ |
| AB |
| BF |
| EF |
∴△AB'B∽△BEF;(3分)
(用相似传递性也可以证明△AB'B∽△BEF,也按步骤分步得分)
当x2=
| 2 |
| 3 |
| 4 |
| 3 |
∵
| BE |
| AE |
| ||
|
| BQ |
| B′Q |
EQ与AB'不平行,
∴△ABB'不是直角三角形,
∴△AB'B与△BEF不相似.(1分)
综上所述,当EF=
| 5 |
| 3 |
当EF=
| 5 |
| 3 |
| 2 |
| 3 |
点评:此题考查了正方形的性质、相切两圆的位置关系、勾股定理、相似三角形及全等三角形的判定和性质等知识的应用能力,综合性强,难度较大.

练习册系列答案
相关题目
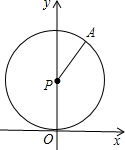 已知:如图,⊙P与x轴切于点O,点P的坐标为(0,1),点A在⊙P上,且在第一象限,∠APO=150°,⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点P的坐标为
已知:如图,⊙P与x轴切于点O,点P的坐标为(0,1),点A在⊙P上,且在第一象限,∠APO=150°,⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点P的坐标为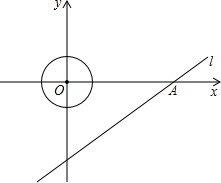 .5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间?
.5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间?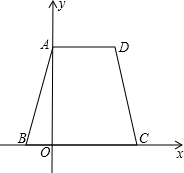 B=2
B=2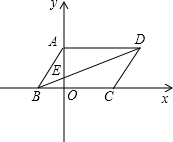 点E,AB=
点E,AB=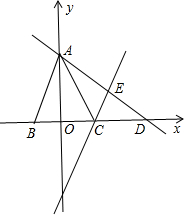 将△AOC沿直线AC折叠,点O落在平面内的点E处,直线AE交x轴于点D.
将△AOC沿直线AC折叠,点O落在平面内的点E处,直线AE交x轴于点D.