题目内容
已知:如图,平行四边形ABCD的边BC在x轴上,点A在y轴的正方向上,对角线BD交y轴于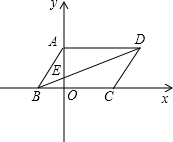 点E,AB=
点E,AB=| 2 |
| 2 |
| 3 |
(1)求点B的坐标;
(2)求过A、B、D三点的抛物线的解析式;
(3)(2)中所求的抛物线上是否存在一点P,使得S△PBD=S?ABCD?若存在,请求出该点坐标;若不存在,请说明理由.
分析:(1)由于∠ADE=∠EBO,可根据∠ADE的正切值求出BO,OE的比例关系,然后在直角三角形AOB中,用勾股定理即可求出OB,OE的长,也就得出了B点的坐标.
(2)由(1)可求出OA的长,也就得出了A,D的坐标,然后根据A、B、D三点的坐标即可用待定系数法求出抛物线的解析式.
(3)可先在x轴上找出一点F(在C点右侧)使得S△FBD=S?ABCD,那么可得出F点的坐标为(3,0),如果过F点坐标BD的平行线,那么平行线上的点与BD组成的三角形的面积就都与平行四边形ABCD的面积相等(这些三角形都以BD为底边,以平行线间的距离为高).那么P点必为此直线与抛物线的交点,可先求出这条直线的解析式然后联立抛物线的解析式来求出P点的坐标.(在y轴两侧各有一个类似F的点,如图).
(2)由(1)可求出OA的长,也就得出了A,D的坐标,然后根据A、B、D三点的坐标即可用待定系数法求出抛物线的解析式.
(3)可先在x轴上找出一点F(在C点右侧)使得S△FBD=S?ABCD,那么可得出F点的坐标为(3,0),如果过F点坐标BD的平行线,那么平行线上的点与BD组成的三角形的面积就都与平行四边形ABCD的面积相等(这些三角形都以BD为底边,以平行线间的距离为高).那么P点必为此直线与抛物线的交点,可先求出这条直线的解析式然后联立抛物线的解析式来求出P点的坐标.(在y轴两侧各有一个类似F的点,如图).
解答:解:(1)∵四边形ABCD是平行四边形,
∴AD∥BO,
∴△BOE∽△DAE
∴
=
,
即
=
∴BO=3EO
在直角三角形ABO中,由AB2=BO2+AO2,
即(
)2=BO2+(
+
BO)2.
整理得5BO2+2BO-7=0,
解得BO=1(负值舍去),
∴B(-1,0).
(2)由(1)知:EO=
BO=
,
∴AO=
+
=1.
∴A(0,1),D(2,1)
设过A、B、D三点的抛物线的解析式为y=ax2+bx+c,
将A、B、D三点的坐标代入,
得:
,
解得
,
y=-
x2+
x+1.
(3)①过F(3,0)作FK∥BD交AD延长线于K,可得K(6,1).
则FK上任一点与BD组成的三角形的面积等于S?ABCD,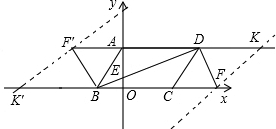
可求得直线FK的解析式为y=
x-1.
解
,
得:
;
.
②过点F′(-2,1)作F′K′∥BD交x轴于K′,可的K′(-5,0).
同样F′K′上的任一点与BD组成的三角形面积等于S?ABCD.
可求得直线F′K′的解析式为y=
x+
.
解
知该方程组无解.
综上所述,满足条件的P点的坐标为(-2,-
)或(3,0).
∴AD∥BO,
∴△BOE∽△DAE
∴
| BO |
| AD |
| EO |
| AE |
即
| BO |
| 2 |
| EO | ||
|
∴BO=3EO
在直角三角形ABO中,由AB2=BO2+AO2,
即(
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
整理得5BO2+2BO-7=0,
解得BO=1(负值舍去),
∴B(-1,0).
(2)由(1)知:EO=
| 1 |
| 3 |
| 1 |
| 3 |
∴AO=
| 2 |
| 3 |
| 1 |
| 3 |
∴A(0,1),D(2,1)
设过A、B、D三点的抛物线的解析式为y=ax2+bx+c,
将A、B、D三点的坐标代入,
得:
|
解得
|
y=-
| 1 |
| 3 |
| 2 |
| 3 |
(3)①过F(3,0)作FK∥BD交AD延长线于K,可得K(6,1).
则FK上任一点与BD组成的三角形的面积等于S?ABCD,

可求得直线FK的解析式为y=
| 1 |
| 3 |
解
|
得:
|
|
②过点F′(-2,1)作F′K′∥BD交x轴于K′,可的K′(-5,0).
同样F′K′上的任一点与BD组成的三角形面积等于S?ABCD.
可求得直线F′K′的解析式为y=
| 1 |
| 3 |
| 5 |
| 3 |
解
|
综上所述,满足条件的P点的坐标为(-2,-
| 5 |
| 3 |
点评:本题着重考查了待定系数法求二次函数解析式、三角形相似、图形面积的求法、平行四边形的性质等知识点,综合性强,能力要求高.考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目



