题目内容
5.若关于x的一元二次方程(k-1)x2+2x-2=0有两个不相等的实数根,那么k的取值范围是k>$\frac{1}{2}$且k≠1.分析 根据方程有两个不相等的实数根利用根的判别式结合二次项系数不为0,即可得出关于k的一元一次不等式组,解不等式组即可得出结论.
解答 解:∵关于x的一元二次方程(k-1)x2+2x-2=0有两个不相等的实数根,
∴$\left\{\begin{array}{l}{△={2}^{2}-4(k-1)×(-2)=8k-4>0}\\{k-1≠0}\end{array}\right.$,
解得:k>$\frac{1}{2}$且k≠1.
故答案为:k>$\frac{1}{2}$且k≠1.
点评 本题考查了根的判别式以及解一元一次不等式组,解题的关键是由方程有两个不等实数根结合二次项系数非0,得出关于k的一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据方程解的个数结合根的判别式得出不等式(不等式组或方程)是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列图形中,轴对称图形的个数( )


| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
17.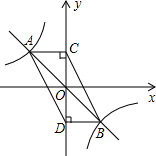 如图,正比例函数y=-x与反比例函数y=-$\frac{2}{x}$的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为C、D,连接AD,BC,则四边形ACBD的面积为( )
如图,正比例函数y=-x与反比例函数y=-$\frac{2}{x}$的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为C、D,连接AD,BC,则四边形ACBD的面积为( )
 如图,正比例函数y=-x与反比例函数y=-$\frac{2}{x}$的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为C、D,连接AD,BC,则四边形ACBD的面积为( )
如图,正比例函数y=-x与反比例函数y=-$\frac{2}{x}$的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为C、D,连接AD,BC,则四边形ACBD的面积为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
14.下列因式分解错误的是( )
| A. | x2-y2=(x+y)(x-y) | B. | x2+y2=(x+y)2 | C. | x2+xy=x(x+y) | D. | x2+6x+9=(x+3)2 |
 如图,抛物线l:y=-x2+bx+c(b,c为常数),其顶点E在正方形ABCD内或边上,已知点A(1,2),B(1,1),C(2,1).
如图,抛物线l:y=-x2+bx+c(b,c为常数),其顶点E在正方形ABCD内或边上,已知点A(1,2),B(1,1),C(2,1). 某校对学生上学方式进行了一次抽样调查,并根据此次调查结果绘制了一个不完整的扇形统计图,其中“其他”部分所对应的圆心角是36°,则“步行”部分所占百分比是40%.
某校对学生上学方式进行了一次抽样调查,并根据此次调查结果绘制了一个不完整的扇形统计图,其中“其他”部分所对应的圆心角是36°,则“步行”部分所占百分比是40%. 如图,在平行四边形ABCD中,点E,F分别为边BC,AD的中点.求证:四边形AECF是平行四边形.
如图,在平行四边形ABCD中,点E,F分别为边BC,AD的中点.求证:四边形AECF是平行四边形.