题目内容
14．分解因式：x2（a-b）+4（b-a）分析 根据提公因式法，可得平方差公式，根据平方差公式，可得答案．
解答 解：原式（a-b）（x2-4）
=（a-b）（x+2）（x-2）．
点评 本题考查了因式分解，提取公因式后利用平方差公式进行二次分解，注意分解要彻底．
练习册系列答案
阅读快车系列答案
相关题目
5．
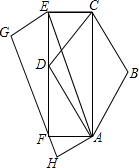如图所示，以菱形ABCD的对角线AC为边作矩形ACEF，使得点D在矩形ACEF的边EF上，再以矩形ACEF的对角线AE为边作平行四边形AEGH，使点F在GH边上，记菱形ABCD的面积为S1，矩形ACEF的面积为S2，平行四边形AEGH的面积为S3，则S1、S2、S3的大小关系是（ ）
如图所示，以菱形ABCD的对角线AC为边作矩形ACEF，使得点D在矩形ACEF的边EF上，再以矩形ACEF的对角线AE为边作平行四边形AEGH，使点F在GH边上，记菱形ABCD的面积为S1，矩形ACEF的面积为S2，平行四边形AEGH的面积为S3，则S1、S2、S3的大小关系是（ ）| A． | S1＞S2＞S3 | B． | S1＜S2＜S3 | C． | S1=S2=S3 | D． | S1＞S2＞S3 |
9．下列各式中最简分式是（ ）
| A． | $\frac{8x}{12y}$ | B． | $\frac{3x}{3x-4}$ | C． | $\frac{a-1}{3a-3}$ | D． | $\frac{b}{2b}$ |