题目内容
10.不要跳步.还有,你千万要注意运算顺序和符号!(1)-16+23+(-17)-(-7)
(2)$-{1^{2010}}×4+{(-2)^4}÷1\frac{1}{3}$
(3)${(-4)^2}-3×{2^2}×(\frac{1}{3}-1)÷(-0.25)$.
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(3)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解答 解:(1)原式=-16+23-17+7=-33+30=-3;
(2)原式=-1×4+16×$\frac{3}{4}$=-4+12=8;
(3)原式=16-3×4×(-$\frac{2}{3}$)×(-4)=16-32=-16.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.在$\frac{22}{7}$,$\sqrt{8}$,-3.1416,π,$\sqrt{25}$,0.161161116…,$\root{3}{9}$中无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
1.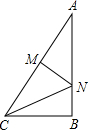 如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )
如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )
 如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )
如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )| A. | $\frac{35}{8}$ | B. | $\frac{25}{4}$ | C. | $\frac{25}{2}$ | D. | 7 |
2.下列事件中,必然事件的是( )
| A. | a是实数,-a2≤0 | |
| B. | 天上打雷后就下雨 | |
| C. | 掷一枚质地均匀的硬币一次,反面朝上 | |
| D. | 某运动员跳高的最好成绩是200.1米 |
20.已知A、B两个动点同时在数轴上匀速运动,且保持运动的方向不变.若A、B两点的起始位置分别用有理数a、b表示,c是最大的负整数,且|a-19c2|+|b-8c3|=0
(1)求a、b、c的值
(2)根据题意及表格中的已知数据,填写完表格:
(3)若A、B两点同时到达点M的位置,且点M用有理数m表示,求m的值
(4)A、B两点能否相距18个单位长度?如果能,求出此时运动了多少秒及此时A、B两点表示的有理数;如果不能,请说明理由.
(1)求a、b、c的值
(2)根据题意及表格中的已知数据,填写完表格:
| 运动时间(秒) | 0 | 5 | 7 | t |
| A点位置 | a | -1 | ||
| B点位置 | b | 17 | 27 |
(4)A、B两点能否相距18个单位长度?如果能,求出此时运动了多少秒及此时A、B两点表示的有理数;如果不能,请说明理由.
 如图,在纸上剪下一个扇形和一个圆形,使之恰好围成一个圆锥,若圆的半径为1cm,若扇形的圆心角等于90°,则扇形的半径为4cm.
如图,在纸上剪下一个扇形和一个圆形,使之恰好围成一个圆锥,若圆的半径为1cm,若扇形的圆心角等于90°,则扇形的半径为4cm.