题目内容
一个三角形三个内角的度数之比为2:3:6,则这个三角形一定是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、钝角三角形 |
考点:三角形内角和定理
专题:
分析:利用三角形内角和定理可求出各内角的度数,再进行判断即可.
解答:解:
由题意可设三个内角分别为2x°,3x°,6x°,
由三角形内角和定理可知:2x+3x+6x=180,解得x=
,
∴6x=
>90,
所以三角形为钝角三角形,
故选D.
由题意可设三个内角分别为2x°,3x°,6x°,
由三角形内角和定理可知:2x+3x+6x=180,解得x=
| 180 |
| 11 |
∴6x=
| 1080 |
| 11 |
所以三角形为钝角三角形,
故选D.
点评:本题主要考查三角形内角和定理,由条件计算出角的大小是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
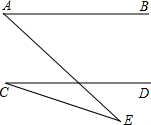 如图,AB∥CD,∠A=50°,∠C=24°,则∠E等于( )
如图,AB∥CD,∠A=50°,∠C=24°,则∠E等于( )| A、70° | B、26° |
| C、36° | D、16° |
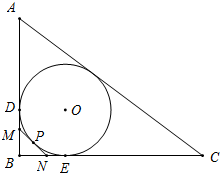 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若AB=6cm,BC=8cm,则Rt△MBN的周长为
如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若AB=6cm,BC=8cm,则Rt△MBN的周长为
