题目内容
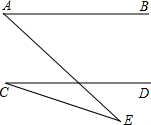如图，AB∥CD，∠A=50°，∠C=24°，则∠E等于（ ）| A、70° | B、26° |
| C、36° | D、16° |
考点：平行线的性质
专题：
分析：根据平行线的性质求出∠AOD，根据三角形外角性质得出∠E=∠AOD-∠C，代入求出即可．
解答：
解：∵AB∥CD，
∴∠A+∠AOD=180°，
∵∠A=50°，
∴∠AOD=130°，
∵∠C=24°，
∴∠E=∠AOD-∠C=26°，
故选B．
解：∵AB∥CD，∴∠A+∠AOD=180°，
∵∠A=50°，
∴∠AOD=130°，
∵∠C=24°，
∴∠E=∠AOD-∠C=26°，
故选B．
点评：本题考查了平行线的性质和三角形外角性质的应用，解此题的关键是求出∠AOD的度数和得出∠E=∠AOD-∠C．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
一个三角形三个内角的度数之比为2：3：6，则这个三角形一定是（ ）
| A、等腰三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、钝角三角形 |
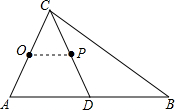如图，在Rt△ABC中，∠ACB=90°，AC=3，AB=5，CD是斜边AB上的中线，以AC为直径作⊙O，设线段CD的中点为P，则点P与⊙O的位置关系是（ ）| A、点P在⊙O内 |
| B、点P在⊙O上 |
| C、点P在⊙O外 |
| D、无法确定 |
以下命题中，真命题的是（ ）
| A、两条直线只有相交和平行两种位置关系 |
| B、同位角相等 |
| C、两边和一角对应相等的两个三角形全等 |
| D、等腰三角形底边中点到两腰的距离相等 |
所示图形中，既是轴对称图形又是中心对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |