题目内容
6. 《九章算术》中记载了这样一道题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的语言表述为:“如果AB为⊙O的直径,弦CD⊥AB于E,AE=1寸,CD=10寸,那么直径AB的长为多少寸?”请你补全示意图,并求出AB的长.
《九章算术》中记载了这样一道题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的语言表述为:“如果AB为⊙O的直径,弦CD⊥AB于E,AE=1寸,CD=10寸,那么直径AB的长为多少寸?”请你补全示意图,并求出AB的长.
分析 连接OD,由直径AB与弦CD垂直,根据垂径定理得到E为CD的中点,由CD的长求出DE的长,设OD=OA=x寸,则AB=2x寸,OE=(x-1)寸,由勾股定理得出方程,解方程求出半径,即可得出直径AB的长.
解答 解:如图所示,连接OD.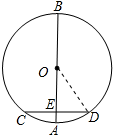
∵弦CD⊥AB,AB为圆O的直径,
∴E为CD的中点,
又∵CD=10寸,
∴CE=DE=$\frac{1}{2}$CD=5寸,
设OD=OA=x寸,则AB=2x寸,OE=(x-1)寸,
由勾股定理得:OE2+DE2=OD2,
即(x-1)2+52=x2,
解得:x=13,
∴AB=26寸,
即直径AB的长为26寸.
点评 此题考查了垂径定理,勾股定理;解答此类题常常利用垂径定理由垂直得中点,进而由弦长的一半,弦心距及圆的半径构造直角三角形,利用勾股定理来解决问题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
14.两个相似三角形的相似比为1:2,若较小三角形的面积为1,则较大三角形的面积为( )
| A. | 8 | B. | 4 | C. | 2 | D. | $\sqrt{2}$ |
11.已知∠A=35°10′48″,则∠A的余角是( )
| A. | 144.82° | B. | 54.82° | C. | 54.42° | D. | 144.42° |
18.计算(-1)2016结果正确的是( )
| A. | -1 | B. | 1 | C. | -2016 | D. | 2016 |
15.在下列分解因式的过程中,分解因式正确的是( )
| A. | -xz+yz=-z(x+y) | B. | 3a2b-2ab2+ab=ab(3a-2b) | ||
| C. | 6xy2-8y3=2y2(3x-4y) | D. | x2+3x-4=(x+2)(x-2)+3x |
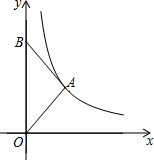 如图,在平面直角坐标系xOy中,点B在y轴上,AB=AO,反比例函数y=$\frac{k}{x}({x>0})$的图象经过点A,若△ABO的面积为2,则k的值为2.
如图,在平面直角坐标系xOy中,点B在y轴上,AB=AO,反比例函数y=$\frac{k}{x}({x>0})$的图象经过点A,若△ABO的面积为2,则k的值为2.