Question

如图，半径不等的两圆相交于A、B两点，线段CD经过点A，且分别交两于C、D两点，连接BC、CD，设P、Q、K分别是BC、BD、CD中点M、N分别是弧BC和弧BD的中点．
求证：①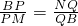；②△KPM∽△NQK．

Answer 1

证明：①如图：连接AB，BM，BN，
∵M是的中点，P是BC的中点，
∴MP⊥BC，∠BPM=90°，
同理NQ⊥BD，∠BQN=90°，
∴∠PBM=∠CAB=（180°-∠DAB）=90°-∠DAB=90°-∠NBD=∠QNB，
∴Rt△BPM∽Rt△NQB，
∴；

②∵P、K是BC、CD中点，
∴KP∥BD，且KP=BD=BQ，
∴四边形PBQK是平行四边形，
∴BP=KQ，BQ=KP，∠BPK=∠BQK，
由①得，
又∵∠KPM=∠KPB+90°=∠KQB+90°=∠NQK，
∴△KPM∽△NQK．
分析：①先连接AB，BM，BN，由于M是的中点，P是BC的中点，那么弧BM等于圆，易知MP⊥BC，∠BPM=90°，同理有NQ⊥BD，∠BQN=90°，再根据圆周角定理易证∠PBM=∠QNB，从而易证Rt△BPM∽Rt△NQB，那么；
②由于P、K是BC、CD中点，根据中位线定理可知KP∥BD，且KP=BD=BQ，根据平行四边形的判定易证
四边形PBQK是平行四边形，于是BP=KQ，BQ=KP，∠BPK=∠BQK，结合①的结论，等量代换有得，根据平行四边形的性质易证∠KPM=∠NQK，从而可证△KPM∽△NQK．
点评：本题考查了圆周所对的圆心角等于90°、相似三角形的判定和性质、平行四边形的判定和性质、三角形中位线定理．