题目内容
在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于D,点F在AC上,点E在BC的延长线上,且CE=CF,连结BF、DE,试问BF、DE的大小关系和位置关系如何?并证明你的结论.
考点:线段垂直平分线的性质
专题:
分析:连接DB,根据DH是AB的垂直平分线得出∠A=∠DBH,再根据三角形外角的性质得出∠CDB=∠A+∠DBH,故可得出CD=CB.由SAS定理得出△ECD≌△FCB,所以ED=FB,∠DEC=∠BFC,∠DEC+∠FBC=90°,进而可得出结论.
解答: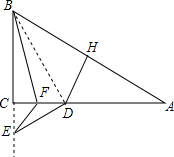 解:BF=DE,且BF⊥DE.理由如下:
解:BF=DE,且BF⊥DE.理由如下:
连接DB.
∵DH是AB的垂直平分线,∠A=22.5°,
∴BD=AD,
∴∠A=∠DBH=22.5°,
∴∠CDB=∠A+∠DBH=45°.
∵∠ACB=90°,
∴∠CBD=45°,
∴CD=CB.
在△ECD和△FCB中
∵
,
∴△ECD≌△FCB(SAS),
∴ED=FB,∠DEC=∠BFC,
∴∠DEC+∠FBC=90°,即ED⊥FB.
 解:BF=DE,且BF⊥DE.理由如下:
解:BF=DE,且BF⊥DE.理由如下:连接DB.
∵DH是AB的垂直平分线,∠A=22.5°,
∴BD=AD,
∴∠A=∠DBH=22.5°,
∴∠CDB=∠A+∠DBH=45°.
∵∠ACB=90°,
∴∠CBD=45°,
∴CD=CB.
在△ECD和△FCB中
∵
|
∴△ECD≌△FCB(SAS),
∴ED=FB,∠DEC=∠BFC,
∴∠DEC+∠FBC=90°,即ED⊥FB.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
如果5个有理数(其中至少有一个正数)的积是负数,那么这五个因数中,正数的个数是( )
| A、1 | B、2或4 | C、5 | D、1或3 |
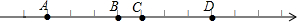 观察图形,数轴上A、B、C、D四点对应的数都是整数,若A点对应的数为a,B点对应的数为b,C点对应的数为c,且2c-3a=11,A在第二个点上,B在第五个点上,C在第六个点上,D在第九个点上,则数轴上的原点是哪一点?
观察图形,数轴上A、B、C、D四点对应的数都是整数,若A点对应的数为a,B点对应的数为b,C点对应的数为c,且2c-3a=11,A在第二个点上,B在第五个点上,C在第六个点上,D在第九个点上,则数轴上的原点是哪一点?