题目内容
(6分)如图①所示,将直尺摆放在三角板ABC上,使直尺与三角板的边分别交于点D,E,F,G,量得∠CGD=42°。
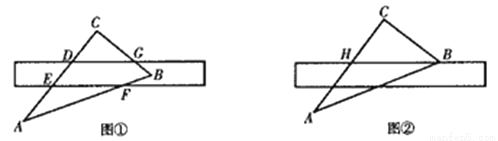
(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示.点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
(1)∠CEF=48°; (2)BC的长为6.96m. 【解析】试题分析:(1)由DG//EF,可知要求∠CEF的度数,需求出∠CDG的度数,而在△CDG在,∠C=90°,∠CGD=42°,从而得解. (2)由已知可得∠CBH=42°,由三角函数即可得; 试题解析:(1)∵ ∠CGD=42°,∠C=90°,∴ ∠CDG=90°- 42°=48°,∵ DG∥EF, ∴∠CEF...
练习册系列答案
相关题目


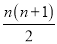 =20 B. n(n-1)=20 C.
=20 B. n(n-1)=20 C. 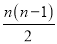 =20 D. n(n+1)=20
=20 D. n(n+1)=20
 B.
B.  C. 4 D. 5
C. 4 D. 5
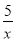 ,当x=-3时,y=___________.
,当x=-3时,y=___________.