题目内容
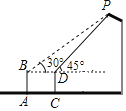
【题目】如图,由10个完全相同的正三角形构成的网格图中,![]() 如图所示,则
如图所示,则![]() =______.
=______.
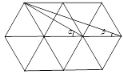
【答案】![]() .
.
【解析】
给图中各点标上字母,连接DE,利用等腰三角形的性质及三角形内角和定理可得出∠α=30°,同理,可得出:∠CDE=∠CED=30°=∠α,由∠AEC=60°结合∠AED=∠AEC+∠CED可得出∠AED=90°,设等边三角形的边长为a,则AE=2a,DE=![]() a,利用勾股定理可得出AD的长,再结合余弦的定义即可求出cos(α+β)的值.
a,利用勾股定理可得出AD的长,再结合余弦的定义即可求出cos(α+β)的值.
给图中各点标上字母,连接DE,如图所示.
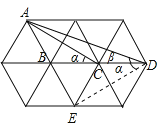
在△ABC中,∠ABC=120°,BA=BC,
∴∠α=30°.
同理,可得出:∠CDE=∠CED=30°=∠α.
又∵∠AEC=60°,
∴∠AED=∠AEC+∠CED=90°.
设等边三角形的边长为a,则AE=2a,DE=2×sin60°a=![]() a,
a,
∴![]() ,
,
∴cos(α+β)=![]() .
.
故答案为:![]() .
.

 阅读快车系列答案
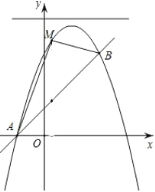
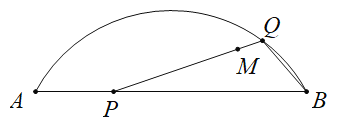
阅读快车系列答案【题目】如图,M是弦![]() 与弧
与弧![]() 所围成的图形的内部的一个定点,P是弦
所围成的图形的内部的一个定点,P是弦![]() 上一动点,连接
上一动点,连接![]() 并延长交弧
并延长交弧![]() 于点Q,连接
于点Q,连接![]() .
.
已知![]() ,设A,P两点间的距离为
,设A,P两点间的距离为![]() ,P,Q两点间距离为
,P,Q两点间距离为![]() ,
,![]() 两点间距离为
两点间距离为![]() .
.
小明根据学习函数的经验,分别对函数![]() 随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
(1)按照如表中自变量x的值进行取点、画图、测量,分别得到了![]() 与x的几组对应值,补全下表:
与x的几组对应值,补全下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 5.24 | 4.24 | 3.24 | 1.54 | 1.79 | 3.47 | |
| 1.31 | 1.34 | 1.42 | 1.54 | 1.80 | 2.45 | 3.47 |
(2)在同一平面直角坐标系![]() 中,描出表中各组数值对应的点
中,描出表中各组数值对应的点![]() 和
和![]() 并画出函数
并画出函数![]() 的图象;
的图象;
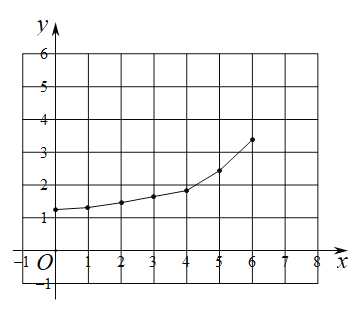
(3)结合函数图象,解决问题:当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度约_________
的长度约_________![]() .(精确到0.1)
.(精确到0.1)
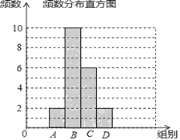
【题目】张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理,绘制了如下不完整的统计图表:
组别 | 步数分组 | 频率 |
A | x<6000 | 0.1 |
B | 6000≤x<7000 | 0.5 |
C | 7000≤x<8000 | m |
D | x≥8000 | n |
合计 | 1 |
根据信息解答下列问题:
(1)填空:m= ,n= ;并补全条形统计图;
(2)这20名朋友一天行走步数的中位数落在 组;(填组别)
(3)张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞,请求出甲、乙被同时点赞的概率.