题目内容
方程x2+(2m-1)x+(m-6)=0有一根不大于-1,另一根不小于1,则该方程两根平方和的最大值是________.
101
分析:设y=x2+(2m-1)x+(m-6),根据有一根不大于-1,另一根不小于1,可列出不等式组,即可解得m的取值范围,再根据根与系数的关系求两根平方和的最大值.
解答:设y=x2+(2m-1)x+(m-6),△=(2m-1)2-4(m-6)=4(m-1)2+21>0,
由方程有一根不大于-1,另一根不小于1,可得不等式组为: ,解得:-4≤m≤2.
,解得:-4≤m≤2.
方程两根平方和为:x12+x22=4m2-6m+13=4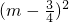 +10
+10 ,
,
∴当m=-4时,有最大值101.
故答案为:101.
点评:本题考查了一元二次方程根与系数的关系及二次函数的最值,难度较大,关键是掌握方程ax2+bx+c=0的两根为x1,x2,则x1+x2=- ,x1•x2=
,x1•x2= .
.
分析:设y=x2+(2m-1)x+(m-6),根据有一根不大于-1,另一根不小于1,可列出不等式组,即可解得m的取值范围,再根据根与系数的关系求两根平方和的最大值.
解答:设y=x2+(2m-1)x+(m-6),△=(2m-1)2-4(m-6)=4(m-1)2+21>0,
由方程有一根不大于-1,另一根不小于1,可得不等式组为:
 ,解得:-4≤m≤2.
,解得:-4≤m≤2.方程两根平方和为:x12+x22=4m2-6m+13=4
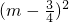 +10
+10 ,
,∴当m=-4时,有最大值101.
故答案为:101.
点评:本题考查了一元二次方程根与系数的关系及二次函数的最值,难度较大,关键是掌握方程ax2+bx+c=0的两根为x1,x2,则x1+x2=-
 ,x1•x2=
,x1•x2= .
. 
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 D,交AB于E,BD、CE相交于点F.
D,交AB于E,BD、CE相交于点F.