题目内容
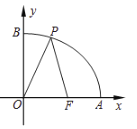
【题目】如图所示，已知点
的坐标为
，点
分别是某函数图象与
轴、
轴的交点，点
是此图象上的一动点．设点的横坐标为，
的长为
，且与之间满足关系：
，则正确结论的序号是（ ）
①
；②
；③当
时，
；④
的最大值是6．
A.①②③B.③④C.①②④D.①④
【答案】D
【解析】
①
，当
运动到与
点重合时，
，
，解之即可. ②当运动到与
点重合时，
，
，在
中运用勾股定理即可求出
.③当
时，代入函数
，解得
，可发现此时
轴，则在
中运用勾股定理求
即可. ④由于
的底
，故当
上的高最大即为时，
有最大值，解之即可.
①正确，
当运动到与点重合时，
，
，
解得
，
所以
，故
.
②错误.
当运动到与点重合时，，，
在中，
.
③错误.
当时，
，
解得，
因为
，
所以轴，
在中，
.
④正确.
由于的底为定值，
故当上的高最大即为时，
有最大值，为
.
故选：D.
全能练考卷系列答案
【题目】某校为改善办学条件，计划购进
、
两种规格的书架，经市场调查发现有线下和线上两种购买方式，具体情况如下表：
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
| 240 | 0 | 210 | 20 |
| 300 | 0 | 250 | 30 |
（1）如果在线下购买、两种书架20个，共花费5880元，求、两种书架各购买了多少个．
（2）如果在线上购买、两种书架20个，共花费
元，设其中种书架购买
个，求span>关于的函数关系式．
（3）在（2）的条件下，若购买种书架的数量不少于种书架的数量，请求出花费最少的购买方案，并计算按照这种购买方案线上比线下节约多少钱．
【题目】某蔬菜专业户试种植了一种紧俏蔬菜（都能卖出），其中每千克的成本
在9元/千克的基础上，还有一些上浮．若浮动价（元/
）与需求量
（千克）成反比，比例系数为30．市场连续四天调查发现，蔬菜售价
（元/）与市场需求量
有如下关系：
需求量 | 50 | 40 | 30 | 20 |
蔬菜售价 | 10 | 15 | 20 | 25 |
（1）直接写出每千克的成本与需求量的关系式_________；
（2）求与的关系式；
（3）当某天的利润率达到
时，求这天的需求量；
（4）求需求量是多少千克时，利润达到最大值，最大值是多少？
【题目】为了让学生掌握知识更加牢固，某校九年级物理组老师们将物理实验的教学方式由之前的理论教学改进为理论+实践，一段时间后，从九年级随机抽取15名学生，对他们在教学方式改进前后的物理实验成绩（百分制）进行整理、描述和分析（成绩用
表示，共分成4组：A．
，B．
，C．
，D．
），下面给出部分信息：
教学方式改进前抽取的学生的成绩在
组中的数据为：80，83，85，87，89．
教学方式改进后抽取的学生成绩为：72，70，76，100，98，100，82，86，95，90，100，86，84，93，88．
教学方式改进前抽取的学生成绩频数分布直方图
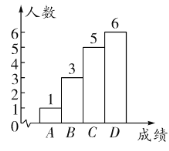
教学方式改进前后抽取的学生成绩对比统计表
统计量 | 改进前 | 改进后 |
平均数 | 88 | 88 |
中位数 |
|
|
众数 | 98 |
|
根据以上信息，解答下列问题：
（1）直接写出上述图表中
的值；
（2）根据以上数据，你认为该校九年级学生的物理实验成绩在教学方式改进前好，还是改进后好？请说明理由（一条理由即可）；
（3）若该校九年级有300名学生，规定物理实验成绩在90分及以上为优秀，估计教学方式改进后成绩为优秀的学生人数是多少？