题目内容
13.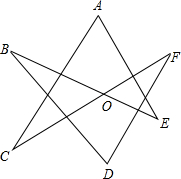 如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F为多少度( )
如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F为多少度( )| A. | 360° | B. | 720° | C. | 540° | D. | 240° |
分析 根据三角形的一个外角等于与它不相邻的两个内角的和求出∠A+∠C,∠B+∠D,再根据邻补角求出∠EOF,然后求解即可.
解答 解:如图,根据三角形的外角性质,∠1=∠A+∠C,∠2=∠B+∠D,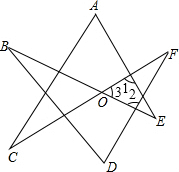
∵∠BOF=120°,
∴∠3=180°-120°=60°,
根据三角形内角和定理,∠E+∠1=180°-60°=120°,
∠F+∠2=180°-60°=120°,
所以,∠1+∠2+∠E+∠F=120°+120°=240°,
即∠A+∠B+∠C+∠D+∠E+∠F=240°.
故选D
点评 本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并把各角进行转化是解题的关键.

练习册系列答案
相关题目
4. 如图,下列各组角中,不是同位角的一组是( )
如图,下列各组角中,不是同位角的一组是( )
 如图,下列各组角中,不是同位角的一组是( )
如图,下列各组角中,不是同位角的一组是( )| A. | ∠1与∠2 | B. | ∠1与∠3 | C. | ∠3与∠4 | D. | ∠1与∠4 |
8.下列各式是一元一次不等式的是( )
| A. | x2-3x+2>4x | B. | $\frac{1}{2}$x+2<x+3 | C. | $\frac{2}{x}$+1≤3x | D. | 2x+3=4x |
5.下列调查适合做普查的是( )
| A. | 了解全球人类男女比例情况 | |
| B. | 了解一批灯泡的平均使用寿命 | |
| C. | 调查20~25岁年轻人最崇拜的偶像 | |
| D. | 对患甲型H7N9的流感患者同一车厢的乘客进行医学检查 |
2.下列二次根式中,与$\sqrt{6}$的乘积为有理数的是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{54}$ |