题目内容
17．
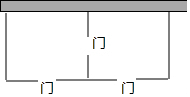某农场拟建两间矩形饲养室，一面靠现有墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门．已知计划中的材料可建墙体（不包括门）总长为21m，则能建成的饲养室总占地面积最大为48m2．
分析 设垂直于墙的材料长为x米，则平行于墙的材料长为21+3-3x=24-3x，表示出总面积S=x（24-3x），最后利用配方法求解即可．
解答 解：设垂直于墙的材料长为x米，则平行于墙的材料长为21+3-3x=24-3x．
则总面积S=x（24-3x）=-3x2+24x=-3（x-4）2+48，故饲养室的最大面积为48平方米．
故答案为：48．
点评 本题考查了二次函数的应用，解题的关键是从实际问题中抽象出函数模型，难度不大．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
7．方程x2=9的解是（ ）
| A． | x=3 | B． | x=-3 | C． | x=±3 | D． | x=±$\sqrt{3}$ |
8．把方程x（x+2）=5化成一般式，则a，b，c的值分别是（ ）
| A． | 1，2，-5 | B． | ．1，2，-10 | C． | ．1，2，5 | D． | ．1，3，2 |
5．关于二次函数y=x2的图象，下列说法错误的是（ ）
| A． | 它的开口向上，且关于y轴对称 | |
| B． | 将它的图象向左平移2个单位后，所得图象的解析式为y=（x-2）2 | |
| C． | 它与y=-x2的图象关于x轴对称 | |
| D． | 当x＞0时，y随x的增大而增大 |
12．抛物线y=x2-1与y轴的交点坐标是（ ）
| A． | （0，1） | B． | （0，-1） | C． | （1，0） | D． | （-1，0） |
2．
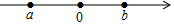实数a，b，在数轴上大致位置如图，则a，b，的大小关系是（ ）
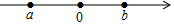实数a，b，在数轴上大致位置如图，则a，b，的大小关系是（ ）| A． | a＜0＜b | B． | b＜a＜0 | C． | 0＜b＜a | D． | a＞0＞b |
7．如图是由一些相同的小正方体构成的几何体的三视图，则构成构成这个几何体的小正方体的个数是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |