题目内容
 已知在平面直角系xOy中,三角形ABC是边长为a的等边三角形,并且边B点始终在y轴上,点C终在x轴上,则OA的最大值是________.
已知在平面直角系xOy中,三角形ABC是边长为a的等边三角形,并且边B点始终在y轴上,点C终在x轴上,则OA的最大值是________.
 a
a分析:取BC的中点D,连接OD、AD,根据直角三角形斜边上的中线等于斜边的一半求出OD的长度,再根据等边三角形的性质可以求出AD的长度,然后根据三角形任意两边之和大于第三边可得点O、D、A三点共线时,OA的长度最大,然后计算即可得解.
解答:
 解:如图,取BC的中点D,连接OD、AD,
解:如图,取BC的中点D,连接OD、AD,则OD=
 BC=
BC= a,
a,AD=
 a,
a,在△OAD中,OD+AD>OA,
所以,当点O、D、A三点共线时,OA的长度最大,
最大值为
 a+
a+ a=
a= a.
a.故答案为:
 a.
a.点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等边三角形的性质,以及三角形的三边关系,作出辅助线构造出三角形是解题的关键.

练习册系列答案
相关题目
 已知在平面直角坐标系xOy中,⊙O的半径为1.
已知在平面直角坐标系xOy中,⊙O的半径为1.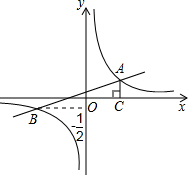 (2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=
(2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=