Question

（2014•静安区一模）已知在平面直角坐标系xOy中，二次函数y=-2x²+bx+c的图象经过点A（-3，0）和点B（0，6）．
（1）求此二次函数的解析式；
（2）将这个二次函数的图象向右平移5个单位后的顶点设为C，直线BC与x轴相交于点D，求∠ABD的正弦值；
（3）在第（2）小题的条件下，联结OC，试探究直线AB与OC的位置关系，并说明理由．

Answer 1

分析：（1）把点A、B的坐标代入函数解析式计算求出b、c的值，即可得解；
（2）先求出抛物线的顶点坐标，再根据向右平移横坐标加，求出点C的坐标，设直线BC的解析式为y=kx+b（k≠0），然后利用待定系数法求出直线BC的解析式，再求出与x轴的交点D的坐标，过点A作AH⊥BD于H，先求出OD，再利用勾股定理列式求出BD，然后求出△ADH和△BDO相似，利用相似三角形对应边成比例列式求出AH，再利用勾股定理，然后根据锐角的正弦等于对边比斜边列式计算即可得解；
（3）方法一：求出

BD

BC

=

AD

AO

，然后根据平行线分线段成比例定理解答；
方法二：过点C作CP⊥x轴于P，分别求出∠BAO和∠COP的正切值，根据正切值相等求出∠BAO=∠COP，再根据同位角相等，两直线平行解答．

解答：解：（1）由题意得，

-2×9-3b+c=0 c=6

，
解得

b=-4 c=6

，
所以，此二次函数的解析式为y=-2x²-4x+6；

（2）∵y=-2x²-4x+6=-2（x+1）²+8，
∴函数y=2x²-4x+6的顶点坐标为（-1，8），
∴向右平移5个单位的后的顶点C（4，8），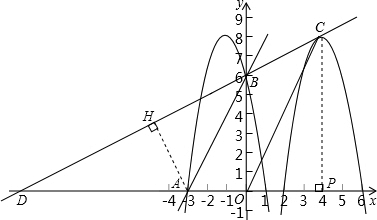
设直线BC的解析式为y=kx+b（k≠0），
则

b=6 4k+b=8

，
解得

k= 1 2 b=6

，
所以，直线BC的解析式为y=

1

2

x+6，
令y=0，则

1

2

x+6=0，
解得x=-12，
∴点D的坐标为（-12，0），
过点A作AH⊥BD于H，
OD=12，BD=

OB2+OD2

=

62+122

=6

5

，
AD=-3-（-12）=-3+12=9，
∵∠ADH=∠BDO，∠AHD=∠BOD=90°，
∴△ADH∽△BDO，
∴

AH

OB

=

AD

BD

，
即

AH

6

=

9

6 5

，
解得AH=

9 5

5

，
∵AB=

OA2+OB2

=

32+62

=3

5

，
∴sin∠ABD=

AH

AB

=

9 5 5

3 5

=

3

5

；

（3）AB∥OC．
理由如下：方法一：∵BD=6

5

，BC=

(4-0)2+(8-6)2

=2

5

，AD=9，AO=3，
∴

BD

BC

=

AD

AO

=3，
∴AB∥OC；
方法二：过点C作CP⊥x轴于P，
由题意得，CP=8，PO=4，AO=3，BO=6，
∴tan∠COP=

CP

OP

=

8

4

=2，
tan∠BAO=

OB

OA

=

6

3

=2，
∴tan∠COP=tan∠BAO，
∴∠BAO=∠COP，
∴AB∥OC．

点评：本题是二次函数综合题，主要利用了待定系数法求二次函数解析式，待定系数法求一次函数解析式，锐角三角函数，相似三角形的判定与性质，作辅助线构造出相似三角形是解题的关键，作出图形更形象直观．