题目内容
 如图,AD是△ABC一边上的高,AD=BD,BE=AC,∠C=75°,求∠ABE的度数.
如图,AD是△ABC一边上的高,AD=BD,BE=AC,∠C=75°,求∠ABE的度数.考点:全等三角形的判定与性质
专题:
分析:根据HL推出Rt△BDE≌Rt△ADC,推出∠C=∠BED=75°,根据等腰三角形的性质和三角形的内角和定理求出∠ABD=∠BAD=45°,∠EBD=15°,即可求出答案.
解答:解:∵AD是△ABC一边上的高,
∴∠BDE=∠ADC=90°,
在Rt△BDE和Rt△ADC中,
,
∴Rt△BDE≌Rt△ADC(HL),
∴∠C=∠BED=75°,
∵∠BDE=90°,AD=BD,
∴∠ABD=∠BAD=45°,∠EBD=15°,
∴∠ABE=∠ABD-∠EBD=45°-15°=30°.
∴∠BDE=∠ADC=90°,
在Rt△BDE和Rt△ADC中,
|
∴Rt△BDE≌Rt△ADC(HL),
∴∠C=∠BED=75°,
∵∠BDE=90°,AD=BD,
∴∠ABD=∠BAD=45°,∠EBD=15°,
∴∠ABE=∠ABD-∠EBD=45°-15°=30°.
点评:本题考查了全等三角形的性质和判定,三角形内角和定理,等腰三角形的性质的应用,解此题的关键是推出△BDE≌△ADC,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
在数轴上-2与2之间的有理数有( )
| A、5个 | B、4个 | C、3个 | D、无数个 |
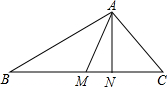 如图所示,AM为△ABC的中线,N在BC上,AB>AC,AC2•BN=AB2•CN,求证:∠BAM=∠CAN.
如图所示,AM为△ABC的中线,N在BC上,AB>AC,AC2•BN=AB2•CN,求证:∠BAM=∠CAN. 已知:如图,四边形ABCD及一点P.求作:四边形A′B′C′D′,使得它是由四边形ABCD绕P点顺时针旋转90°得到的.(不写作法保留作图痕迹)
已知:如图,四边形ABCD及一点P.求作:四边形A′B′C′D′,使得它是由四边形ABCD绕P点顺时针旋转90°得到的.(不写作法保留作图痕迹)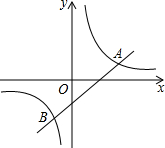 如图,已知反比例函数y=
如图,已知反比例函数y=