题目内容
若四条直线x=1，y=-1，y=3，y=kx-3所围成的凸四边形的面积等于12，则k的值为________．
-2或1
分析：本题可先求出直线y=kx-3与y=-1和y=3的交点坐标，由于四条直线所围的图形为直角梯形，也就求出了梯形上下底和高的长．根据直角梯形的面积公式可得出关于k的方程，即可求出k的值．
解答：在y=kx-3中，令y=-1，
解得x=
；
令y=3，x=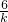
；
当k＜0时，四边形的面积是：
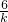[（1-）+（1-）]×4=12，
解得k=-2；
当k＞0时，可得[（-1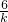）+（-1）]×4=12，
解得k=1．
即k的值为-2或1；
故答案为：-2或1．
点评：此题考查了一次函数的综合；利用k正确表示出四边形的面积是解决本题的关键，由于k的符号不确定，因此要分类讨论，以免造成错解、漏解．
分析：本题可先求出直线y=kx-3与y=-1和y=3的交点坐标，由于四条直线所围的图形为直角梯形，也就求出了梯形上下底和高的长．根据直角梯形的面积公式可得出关于k的方程，即可求出k的值．
解答：在y=kx-3中，令y=-1，
解得x=
；令y=3，x=
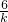；当k＜0时，四边形的面积是：
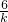[（1-）+（1-）]×4=12，解得k=-2；
当k＞0时，可得
[（-1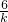）+（-1）]×4=12，解得k=1．
即k的值为-2或1；
故答案为：-2或1．
点评：此题考查了一次函数的综合；利用k正确表示出四边形的面积是解决本题的关键，由于k的符号不确定，因此要分类讨论，以免造成错解、漏解．
练习册系列答案
相关题目
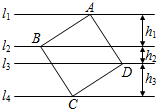之间的距离依次为h1、h2、h3（h1＞0，h2＞0，h3＞0）．
线上，正方形ABCD的面积为S．