题目内容
 如图,在等边△ABC中,点D、E分别为AB、AC边的中点,点F为BC边上一点,CF=1,连接DF,以DF为边作等边△DFG,连接AG,且∠DAG=90°,则线段EF的长为________.
如图,在等边△ABC中,点D、E分别为AB、AC边的中点,点F为BC边上一点,CF=1,连接DF,以DF为边作等边△DFG,连接AG,且∠DAG=90°,则线段EF的长为________.

分析:连接DE,根据等边三角形性质得出AB=AC=BC,∠B=∠C=∠BAC=60°,根据三角形的中位线求出AD
 AB,AE=
AB,AE= AC,得出△ADE是等边三角形,推出AD=DE,∠ADE=∠AED=∠DAE=60°,求出∠ADG=∠EDF,证△ADG≌△EDF,推出∠DAG=∠DEF,求出∠EFC=∠DEF=90°,根据勾股定理求出即可.
AC,得出△ADE是等边三角形,推出AD=DE,∠ADE=∠AED=∠DAE=60°,求出∠ADG=∠EDF,证△ADG≌△EDF,推出∠DAG=∠DEF,求出∠EFC=∠DEF=90°,根据勾股定理求出即可.解答:连接DE,

∵△ABC是等边三角形,
∴AB=BC=AC,○B=∠C=∠BAC=60°,
∵D、E分别为AB、AC中点,
∴AD
 AB,AE=
AB,AE= AC,
AC,∴DE∥BC,AD=AE,
∴△ADE是等边三角形,
∴AD=DE,∠ADE=∠AED=∠DAE=60°,
∴∠ADG+∠GDE=60°,
∵△DFG是等边三角形,
∴DG=DF,∠GDF=∠EDG+∠EDF=60°,
∴∠ADG=∠EDF,
在△ADG和△EDF中

∴△ADG≌△EDF(SAS),
∴∠DAG=∠DEF,
∵∠DAG=90°,
∴∠DEF=90°,
∵DE∥BC,
∴∠EFC=∠DEF=90°,
∵CF=1,∠C=60°,
∴∠CEF=30°,
∴CE=2,由勾股定理得:EF=
 ,
,故答案为:
 .
.点评:本题考查了等边三角形的性质和判定,勾股定理,三角形的中位线,全等三角形的性质和判定的应用,主要考查学生综合运用定理进行推理的能力.

练习册系列答案
相关题目
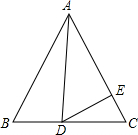 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
 16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是
16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是 21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.
21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°. 如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm.
如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm. 如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证:
如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证: