题目内容
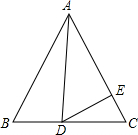
 如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm.
如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm.(1)求BE的长;
(2)△BDE是什么三角形,为什么?
分析:(1)首先根据等边三角形的性质知AB=AC=BC=10cm,再由D是AC的中点,CE=CD,得到CE=5cm,进而求出BE的长;
(2)根据等边三角形的性质得∠ABC=∠ACB=60°,∠DBC=
∠ABC=30°,结合CD=CE,以及角角之间的等量关系,得到∠DBE=∠CED,即可求出BD=ED,进而得出答案.
(2)根据等边三角形的性质得∠ABC=∠ACB=60°,∠DBC=
| 1 |
| 2 |
解答:解:(1)∵△ABC是等边三角形,
∴AB=AC=BC=10cm,
∵D是AC的中点,
∴CD=
AC=5cm,
又∵CD=CE,
∴CE=5cm,
∴BE=BC+CE=10+5=15(cm),
(2)△BDE是等腰三角形,
理由如下:
∵△ABC是等边三角形,D是AC的中点,
∴∠ABC=∠ACB=60°,∠DBC=
∠ABC=30°,
又∵CD=CE,
∴∠EDC=∠CED,
又∵∠ACB=∠CDE+∠CED,
∴∠CED=
∠ACB=30°,
∴∠DBE=∠CED,
∴BD=ED,
∴△BDE是等腰三角形.
∴AB=AC=BC=10cm,
∵D是AC的中点,
∴CD=
| 1 |
| 2 |
又∵CD=CE,
∴CE=5cm,
∴BE=BC+CE=10+5=15(cm),
(2)△BDE是等腰三角形,
理由如下:
∵△ABC是等边三角形,D是AC的中点,
∴∠ABC=∠ACB=60°,∠DBC=
| 1 |
| 2 |
又∵CD=CE,
∴∠EDC=∠CED,
又∵∠ACB=∠CDE+∠CED,
∴∠CED=
| 1 |
| 2 |
∴∠DBE=∠CED,
∴BD=ED,
∴△BDE是等腰三角形.
点评:本题主要考查等边三角形的性质的知识点,解答本题的关键是熟练掌握等边三角形边角之间的关系,此题难度一般.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
 16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是
16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是 21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.
21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°. 如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证:
如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证: