Question

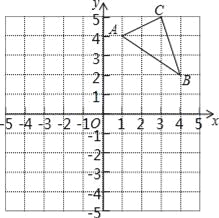
【题目】如图1，在平面直角坐标系中，点 O 是坐标原点，四边形 ABCO 是菱形，点 A 的坐标为（－3，4），点 C 在 x 轴的正半轴上，直线 AC 交 y 轴于点 M，AB 边交 y 轴于点 H．

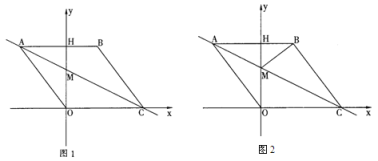
（1）求直线 AC 的解析式；

（2）连接 BM，如图 2，动点 P 从点 A 出发，沿折线 ABC 方向以 2 个单位／秒的速度向终点 C 匀速运动，设△PMB 的面积为 S（S≠0），点 P 的运动时间为t 秒，求 S 与 t 之间的函数关系式（要求写出自变量 t 的取值范围）.

Answer 1

【答案】（1）；（2）．

【解析】

（1）已知A点的坐标，就可以求出OA的长，根据OA=OC，就可以得到C点的坐标，根据待定系数法就可以求出函数解析式．

（2）点P的位置应分P在AB和BC上，两种情况进行讨论．当P在AB上时，△PMB的底边PB可以用时间t表示出来，高是MH的长，因而面积就可以表示出来．

（1）过点A作AE⊥x轴垂足为E，如图（1）．

∵A（﹣3，4），∴AE=4 OE=3，∴OA5．

∵四边形ABCO为菱形，∴OC=CB=BA=0A=5，∴C（5，0）

设直线AC的解析式为：y=kx+b．

∵，∴，∴直线AC的解析式为．

（2）由（1）得M点坐标为（0，），∴OM，如图（1），分两种情况讨论：

①当P点在AB边上运动时

由题意得OH=4，∴HM=OH﹣OM=4，∴SBPMH（5﹣2t），∴St（0≤t）；

②当P点在BC边上运动时，记为P1．

∵∠OCM=∠BCM，CO=CB，CM=CM，∴△OMC≌△BMC，∴OM=BM，∠MOC=∠MBC=90°，∴SP1BBM（2t﹣5），∴St（t≤5）．

综上所述：．