Question

【题目】如图，已知抛物线y=（x+2）（x﹣4）（k为常数，且k＞0）与x轴从左至右依次交于A，B两点，与y轴交于点C，经过点B的直线y=﹣x+b与抛物线的另一交点为D．

（1）若点D的横坐标为﹣5，求抛物线的函数表达式；

（2）若在第一象限内的抛物线上有点P，使得以A，B，P为顶点的三角形与△ABC相似，求k的值；

（3）在（1）的条件下，设F为线段BD上一点（不含端点），连接AF，一动点M从点A出发，沿线段AF以每秒1个单位的速度运动到F，再沿线段FD以每秒2个单位的速度运动到D后停止，当点F的坐标是多少时，点M在整个运动过程中用时最少？

Answer 1

【答案】（1）抛物线的函数表达式为：y=（x+2）（x﹣4）；

（2）k=或k=；

（3）当点F坐标为（﹣2，2）时，点M在整个运动过程中用时最少．

【解析】

试题分析：（1）首先求出点A、B坐标，然后求出直线BD的解析式，求得点D坐标，代入抛物线解析式，求得k的值；

（2）因为点P在第一象限内的抛物线上，所以∠ABP为钝角．因此若两个三角形相似，只可能是△ABC∽△APB或△ABC∽△PAB．如答图2，按照以上两种情况进行分类讨论，分别计算；

（3）由题意，动点M运动的路径为折线AF+DF，运动时间：t=AF+DF．如答图3，作辅助线，将AF+DF转化为AF+FG；再由垂线段最短，得到垂线段AH与直线BD的交点，即为所求的F点．

试题解析：（1）抛物线y=（x+2）（x﹣4），

令y=0，解得x=﹣2或x=4，

∴A（﹣2，0），B（4，0）．

∵直线y=﹣x+b经过点B（4，0），

∴﹣×4+b=0，解得b=，

∴直线BD解析式为：y=﹣x+．

当x=﹣5时，y=3，

∴D（﹣5，3）．

∵点D（﹣5，3）在抛物线y=（x+2）（x﹣4）上，

∴（﹣5+2）（﹣5﹣4）=3，

∴k=．

∴抛物线的函数表达式为：y=（x+2）（x﹣4）．

（2）由抛物线解析式，令x=0，得y=﹣k，

∴C（0，﹣k），OC=k．

因为点P在第一象限内的抛物线上，所以∠ABP为钝角．

因此若两个三角形相似，只可能是△ABC∽△APB或△ABC∽△PAB．

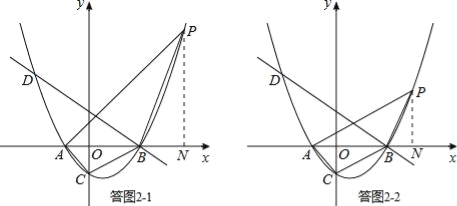
①若△ABC∽△APB，则有∠BAC=∠PAB，如答图2﹣1所示．

设P（x，y），过点P作PN⊥x轴于点N，则ON=x，PN=y．

tan∠BAC=tan∠PAB，即：，

∴．

∴P（x，），代入抛物线解析式y=（x+2）（x﹣4），

得（x+2）（x﹣4）=x+k，整理得：x2﹣6x﹣16=0，

解得：x=8或x=﹣2（与点A重合，舍去），

∴P（8，5k）．

∵△ABC∽△APB，

∴，即，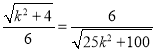

解得：k=．

②若△ABC∽△PAB，则有∠ABC=∠PAB，如答图2﹣2所示．

与①同理，可求得：k=．

综上所述，k=或k=．

（3）如答图3，由（1）知：D（﹣5，3），

如答图2﹣2，过点D作DN⊥x轴于点N，则DN=3，ON=5，BN=4+5=9，

∴tan∠DBA=，

∴∠DBA=30°．

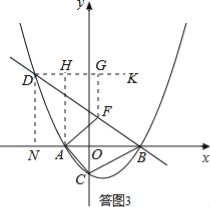
过点D作DK∥x轴，则∠KDF=∠DBA=30°．

过点F作FG⊥DK于点G，则FG=DF．

由题意，动点M运动的路径为折线AF+DF，运动时间：t=AF+DF，

∴t=AF+FG，即运动的时间值等于折线AF+FG的长度值．

由垂线段最短可知，折线AF+FG的长度的最小值为DK与x轴之间的垂线段．

过点A作AH⊥DK于点H，则t最小=AH，AH与直线BD的交点，即为所求之F点．

∵A点横坐标为﹣2，直线BD解析式为：y=﹣x+，

∴y=﹣×（﹣2）+=2，

∴F（﹣2，2）．

综上所述，当点F坐标为（﹣2，2）时，点M在整个运动过程中用时最少．