Question

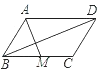
【题目】如图，平行四边形的对角线，相交于点，延长到，使，连接．

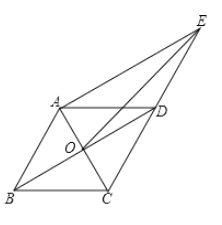
(1)求证：四边形是平行四边形；

(2)连接，若，且，求的长．

Answer 1

【答案】(1)证明间解析；（2）

【解析】

(1)四边形ABCD是平行四边形，由平行四边形的性质，及，可得AB=DE， AB//DE ，则四边形ABDE是平行四边形；

(2)因为AD=DE=8，则AD=AB=8，四边形ABCD是菱形，由菱形的性质及解直角三角形可得AO=ABsin∠ABO=4，BO=ABcos∠ABO=4， BD=8 ，则AE=BD，利用勾股定理可得OE．

（1）证明：∵四边形ABCD是平行四边形，

∴AB∥CD，AB＝CD．

∵DE＝CD，

∴AB＝DE．

又∵AB∥DE

∴四边形ABDE是平行四边形；

（2）∵AD＝DE＝8，

∴AD＝AB＝8．

∴ABCD是菱形，

∴AB＝BC，AC⊥BD，，．

又∵∠ABC＝60°，

∴∠ABO＝30°．

在Rt△ABO中，，．

∴．

∵四边形ABDE是平行四边形，

∴AE∥BD，．

又∵AC⊥BD，

∴AC⊥AE．

在Rt△AOE中，．