题目内容
9.已知直线y=kx-4经过点(4,4),求不等式kx-4≥0的解集.分析 把点的坐标代入函数解析式求出k值,再求出直线与x轴的交点坐标,然后根据一次函数的增减性写出不等式的解集即可.
解答 解:∵直线y=kx-4经过点(4,4),
∴4k-4=4,
∴k=2,
∴直线解析式为y=2x-4,
令y=0,则2x-4=0,
解得x=2,
∵k=2>0,
∴y随x的增大而增大,
∴不等式kx-4≥0的解集是x≥2.
点评 本题考查了一次函数与一元一次不等式,主要利用了待定系数法求函数解析式,一次函数的增减性,是基础题,求出k值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知关于x的一元二次方程(k-2)2x2+(2k+1)x+1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>$\frac{4}{3}$且k≠2 | B. | k≥$\frac{4}{3}$且k≠2 | C. | k>$\frac{3}{4}$且k≠2 | D. | k≥$\frac{3}{4}$且k≠2 |
5.已知P是△ABC的边AC上一点,连接BP,则下列不能判定△ABP∽△ACB的是( )
| A. | ∠ABP=∠C | B. | ∠APB=∠ABC | C. | $\frac{AB}{AP}$=$\frac{AC}{AB}$ | D. | $\frac{AB}{BP}$=$\frac{AC}{BC}$ |
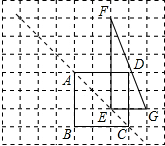 如图,方格纸中每个小正方形的边长均为1,正方形ABCD和△EFG的顶点都在小正方形的顶点上.
如图,方格纸中每个小正方形的边长均为1,正方形ABCD和△EFG的顶点都在小正方形的顶点上. 如图,已知直线上两点坐标,请求出这条直线的解析式,并判断点A(2,-6),B(3,-10),C(-2,5)是否坐此直线上?
如图,已知直线上两点坐标,请求出这条直线的解析式,并判断点A(2,-6),B(3,-10),C(-2,5)是否坐此直线上? 一天晚上,小伟帮妈妈清洗茶杯,三个茶杯只有花色不同,其中一个无盖(如图),在清洗过程中,突然停电了,小伟只好摸黑清洗
一天晚上,小伟帮妈妈清洗茶杯,三个茶杯只有花色不同,其中一个无盖(如图),在清洗过程中,突然停电了,小伟只好摸黑清洗