题目内容
已知a,b,c满足(a-
)2+
+|c-2
|=0,
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能构成三角形,求出三角形的周长和面积;若不能构成三角形,请说明理由.
| 5 |
| b-5 |
| 5 |
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能构成三角形,求出三角形的周长和面积;若不能构成三角形,请说明理由.
考点:勾股定理的逆定理,非负数的性质:绝对值,非负数的性质:偶次方,非负数的性质:算术平方根
专题:
分析:(1)直接根据非负数的性质求出a、b、c的值即可;
(2)先根据勾股定理的逆定理判断出三角形的形状,再求出其周长和面积即可.
(2)先根据勾股定理的逆定理判断出三角形的形状,再求出其周长和面积即可.
解答:解:(1)∵a,b,c满足(a-
)2+
+|c-2
|=0,
∴a-
=0,b-5=0,c-2
=0,
∴a=
,b=5,c=2
;
(2)能.
∵由(1)知a=
,b=5,c=2
,
∴a2=5,b2=25,c2=20.
∵5+20=25,
∴a2+c2=b2,
∴此三角形是直角三角形,
∴三角形的周长=
+5+2
=3
+5;
三角形的面积=
×
×5=
.
| 5 |
| b-5 |
| 5 |
∴a-
| 5 |
| 5 |
∴a=
| 5 |
| 5 |
(2)能.
∵由(1)知a=
| 5 |
| 5 |
∴a2=5,b2=25,c2=20.
∵5+20=25,
∴a2+c2=b2,
∴此三角形是直角三角形,
∴三角形的周长=
| 5 |
| 5 |
| 5 |
三角形的面积=
| 1 |
| 2 |
| 5 |
5
| ||
| 2 |
点评:本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
相关题目
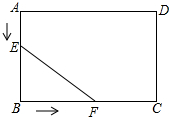 如图,在矩形ABCD中,AB=6cm,BC=8cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达C点时,两点同时停止运动,问经过几秒后△EBF的面积为5cm2?
如图,在矩形ABCD中,AB=6cm,BC=8cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达C点时,两点同时停止运动,问经过几秒后△EBF的面积为5cm2?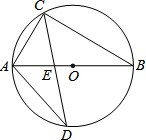 如图,已知点C是直径为AB的⊙O上的点,AC=5cm,∠ABC=30°,∠ACB的平分线交⊙O于D,求CD的长.
如图,已知点C是直径为AB的⊙O上的点,AC=5cm,∠ABC=30°,∠ACB的平分线交⊙O于D,求CD的长.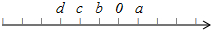 有理数a,b,c,d,在数轴上的位置一条轴,有5个点,距离相等,第一个点表示d,第二个点表示c,第3个点表示b,第4个点表示0,第5个点表示a.
有理数a,b,c,d,在数轴上的位置一条轴,有5个点,距离相等,第一个点表示d,第二个点表示c,第3个点表示b,第4个点表示0,第5个点表示a.