题目内容
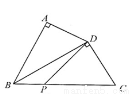
(10分)如图,AB是⊙O的直径,C为⊙O上一点,过点B作经过点C的直线CD的垂线,垂足为E(即BE⊥CD),BE交⊙O于点F,且BC平分∠ABE.

(1)求证:CD为⊙O的切线;
(2)若AB=10,CE=4,求线段EF的长.
(1)连接OC证CD⊥OC(2)EF=2
【解析】
试题分析:(1)连接OC,证CD⊥OC即可,因为BE⊥CD,所以只要证OC∥BE即可,而根据等边对等角,以及角平分线的定义,即可证得∠OCB=∠EBC,则OC∥BE;(2)连接AC,则△ABC∽△CBE,设AC=x,  ,由勾股定理可得
,由勾股定理可得 ,由图知AC<BC,所以
,由图知AC<BC,所以 ,BC=
,BC= ,BE=8,由切割线定理可求出EF.
,BE=8,由切割线定理可求出EF.
试题解析:(1)连接OC.∵OC=OB,∴∠ABC=∠OCB,又∵∠EBC=∠ABC,∴∠OCB=∠EBC,∴OC∥BE,∵BE⊥CD,∴OC⊥CD,∴CD是⊙O的切线;(2)连接AC,因为AB是直径,所以∠ACB=90°, 又BC平分∠ABE所以△ABC∽△CBE,设AC=x, 所以 ,由勾股定理可得
,由勾股定理可得 ,由图知AC<BC,所以
,由图知AC<BC,所以 ,BC=
,BC= ,BE=8,由切割线定理得:
,BE=8,由切割线定理得: ,所以
,所以 ,所以EF=2.
,所以EF=2.
考点:1.切线的判定;2.勾股定理;3.相似三角形的性质与判定;4.切割线定理.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
在棱柱中( )
| A.只有两个面平行 |
| B.所有的棱都平行 |
| C.所有的面都是平行四边形 |
| D.两底面平行,且各侧棱也互相平行 |