题目内容
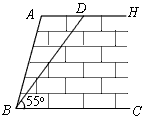
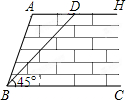如图，某拦河坝截面的原设计方案为：AH∥BC，坡角∠ABC=60°，坝顶到坝脚的距离AB=6m．为了提高拦河坝的安全性，现将坡角改为45°，由此，点A需向右平移至点D，请你计算AD的长（精确到0.1m）．分析：此题可先利用坡角正弦值求得堤坝的高，再利用坡角的余弦值求得AB的水平距离，利用坡角的正切值求得BD的水平距离，则AD由二者相减可得．
解答：
解：过点A作AN⊥BC，过D点D作DM⊥BC，
由坡角∠ABC=60°，坝顶到坝脚AB的长为6m，
则BN=AB•cos60°，AD=MN，BM=DM=AN=AB•sin60°，
则AD=BM-MN=AB•sin60°-AB•cos60°=3
-3≈2.2（m）．
答：AD的长约为2.2米．
解：过点A作AN⊥BC，过D点D作DM⊥BC，由坡角∠ABC=60°，坝顶到坝脚AB的长为6m，
则BN=AB•cos60°，AD=MN，BM=DM=AN=AB•sin60°，
则AD=BM-MN=AB•sin60°-AB•cos60°=3
| 3 |
答：AD的长约为2.2米．
点评：此题主要考查学生对坡度坡角的掌握及三角函数的运用能力．结合图形得出梯形的高是解题关键．
练习册系列答案
相关题目
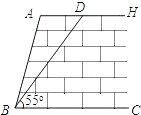如图，某拦河坝截面的原设计方案为：AH∥BC，坡角∠ABC=74°，坝顶到坝脚的距离AB=6m．为了提高拦河坝的安全性，现将坡角改为55°，由此，点A需向右平移至点D，请你计算AD的长．（精确到0.1m）
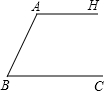安全性，现将坡角改为45°，为此，点A需向右平移至点D．