题目内容
 如图,梯形ABCD中,AB∥DC,∠B=90°,E为BC上一点,且AE⊥ED.若BC=12,DC=7,BE:EC=1:2,
如图,梯形ABCD中,AB∥DC,∠B=90°,E为BC上一点,且AE⊥ED.若BC=12,DC=7,BE:EC=1:2,
(1)求AB的长.
(2)求△AED的面积.
解:(1)∵AB∥DC,且∠B=90°,
∴∠AEB+∠BAE=90°及∠C=90度.
∴∠AEB+∠CED=90度.
故∠BAE=∠CED.
∴△EAB∽△DEC.
∴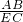 =
=
又BE:EC=1:2,且BC=12及DC=7,
故 =
=
则AB=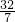 .
.
(2)∵△EAB∽△DEC,
∴
即: =
=
解得:CD=7
∴S△AED=S梯形ABCD-S△ABE-S△ECD= (AB+CD)•BC-
(AB+CD)•BC- AB•BE-
AB•BE- EC•CD=
EC•CD= (
(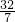 +7)•12-
+7)•12- ×
×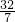 ×4-
×4- ×8×7=
×8×7=
分析:(1)由题意易知AB和CD所在的两个三角形相似,再利用相似比即可求出所求线段的长度.
(2)根据证得的△EAB∽△DEC利用相似三角形对应边的比成比例求得线段CD的长,利用梯形的面积减去两个三角形的面积即可求得三角形AED的面积.
点评:本题考查了相似三角形的性质及判定,解题的关键是正确的利用相似三角形的对应边成比例求得相应的线段的长.
∴∠AEB+∠BAE=90°及∠C=90度.
∴∠AEB+∠CED=90度.
故∠BAE=∠CED.
∴△EAB∽△DEC.
∴
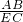 =
=
又BE:EC=1:2,且BC=12及DC=7,
故
 =
=
则AB=
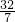 .
.(2)∵△EAB∽△DEC,
∴

即:
 =
=
解得:CD=7
∴S△AED=S梯形ABCD-S△ABE-S△ECD=
 (AB+CD)•BC-
(AB+CD)•BC- AB•BE-
AB•BE- EC•CD=
EC•CD= (
(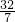 +7)•12-
+7)•12- ×
×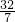 ×4-
×4- ×8×7=
×8×7=
分析:(1)由题意易知AB和CD所在的两个三角形相似,再利用相似比即可求出所求线段的长度.
(2)根据证得的△EAB∽△DEC利用相似三角形对应边的比成比例求得线段CD的长,利用梯形的面积减去两个三角形的面积即可求得三角形AED的面积.
点评:本题考查了相似三角形的性质及判定,解题的关键是正确的利用相似三角形的对应边成比例求得相应的线段的长.

练习册系列答案
相关题目
 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2, 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.