题目内容
“玉女峰”是武夷山最秀丽的山峰,她亭亭玉立于九曲溪边,为测得峰顶A到河面B的 高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).
高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).
(1)用含α、β和m的式子表示;
(2)当α=48°,β=66°,m=50米时,求h的值.(精确到1米)
解:(1)用含α、β和m的式子表示h:在Rt△ABC中,∵tanα= ,∴BC=
,∴BC=
在Rt△ABD中,∵ ,∴
,∴
∵m=BC-BD,∴
∴ ;
;
(2)当m=50,α=48°,β=66°时,h= ≈100(米).
≈100(米).
答:h的值约为100米.
分析:(1)可分别在Rt△ABC和Rt△ABD中,用AB表示出BC、BD的长,进而由CD=BC-BD=m得到AB即h的表达式;
(2)将题目给出的值代入(1)得到的关系式中,即可求得h的值.
点评:本题考查直角三角形的解法,首先构造直角三角形,再借助角边关系、三角函数的定义解题.
 ,∴BC=
,∴BC=
在Rt△ABD中,∵
 ,∴
,∴
∵m=BC-BD,∴

∴
 ;
;(2)当m=50,α=48°,β=66°时,h=
 ≈100(米).
≈100(米).答:h的值约为100米.
分析:(1)可分别在Rt△ABC和Rt△ABD中,用AB表示出BC、BD的长,进而由CD=BC-BD=m得到AB即h的表达式;
(2)将题目给出的值代入(1)得到的关系式中,即可求得h的值.
点评:本题考查直角三角形的解法,首先构造直角三角形,再借助角边关系、三角函数的定义解题.

练习册系列答案
相关题目
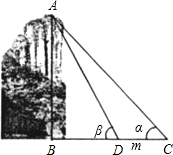 高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).
高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).
