题目内容
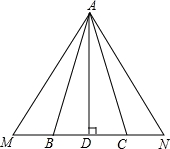
如图，在△ABC中，AD⊥BC于D，点M、N分别在BC所在的直线上，且AB=AC，BM=CN，试判断△AMN的形状，并说明理由．
【考点】等腰三角形的判定．
【分析】根据等腰三角形的性质可以得出∠ABC=∠ACB，再由平角的性质可以得出∠ABM=∠ACN，就可以得出△AMB≌△ANC，就可以得出结论．
【解答】解：等腰三角形，理由如下，
∵AB=AC，
∴∠ABC=∠ACB．
∵∠ABC+∠ABM=180°，∠ACB+∠ACN=180°，
∴∠ABM=∠ACN．
在△AMB和△ANC中，
，
∴△AMB≌△ANC（ASA），
∴AM=AN，
∴△AMN是等腰三角形．
【点评】本题考查了等腰三角形的性质的运用，平角的性质的运用，全等三角形的判定与性质的运用，解答时证明三角形全等是关键．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
是等腰直角三角形，BC=AB，A点在x负半轴上，直角顶点B在y轴上，点C在x轴上方．
