题目内容
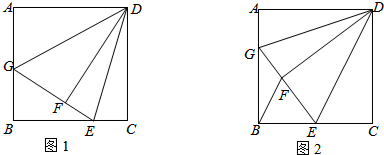
如图．已知∠AED=∠ACB，∠3=∠B．试判断∠1与∠2的数量关系，并说明理由．考点：平行线的判定与性质
专题：常规题型
分析：由∠AED=∠ACB，根据同位角相等，两直线平行得DE∥BC，则根据平行线的性质得∠B=∠ADE，再利用等量代换得到∠3=∠ADE，于是可根据平行线的判定得AB∥EF，所以∠2=∠4，由于∠1+∠4=180°，所以∠1+∠2=180°．
解答：解：∠1+∠2=180°．理由如下：
∵∠AED=∠ACB，
∴DE∥BC，
∴∠B=∠ADE，
∵∠3=∠B，
∴∠3=∠ADE，
∴AB∥EF，
∴∠2=∠4，
而∠1+∠4=180°，
∴∠1+∠2=180°．
∵∠AED=∠ACB，
∴DE∥BC，
∴∠B=∠ADE，
∵∠3=∠B，
∴∠3=∠ADE，
∴AB∥EF，
∴∠2=∠4，
而∠1+∠4=180°，
∴∠1+∠2=180°．
点评：本题考查了平行线的判定与性质：同位角相等，两直线平行；内错角相等，两直线平行；两直线平行，同位角相等；两直线平行，内错角相等．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
在平面直角坐标系中，将点P（-2，1）向右平移3个单位长度，得到点P′的坐标是（ ）
| A、（-2，4） |
| B、（1，1） |
| C、（-2，-2） |
| D、（-5，1） |
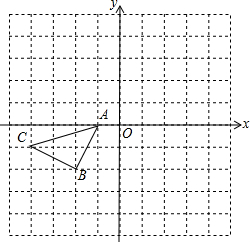如图的正方形格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：