题目内容
17.关于x的一元二次方程x2-3x+m-1=0的两个实数根分别为x1,x2.(1)求m的取值范围;
(2)若3(x1+x2)-x1x2-10=0,求m的值.
分析 (1)由方程有两个实数根,即可得出△=13-4m≥0,解之即可得出m的取值范围;
(2)由根与系数的关系可得出x1+x2=3、x1x2=m-1,结合3(x1+x2)-x1x2-10=0可得出关于m的一元一次方程,解之即可得出m的值.
解答 解:(1)∵关于x的一元二次方程x2-3x+m-1=0有两个实数根,
∴△=(-3)2-4(m-1)=13-4m≥0,
解得:m≤$\frac{13}{4}$.
(2)∵关于x的一元二次方程x2-3x+m-1=0的两个实数根分别为x1,x2,
∴x1+x2=3,x1x2=m-1,
∴3(x1+x2)-x1x2-10=3×3-(m-1)-10=0,
解得:m=0.
∴当3(x1+x2)-x1x2-10=0时,m的值为0.
点评 本题考查了根与系数的关系以及根的判别式,解题的关键是:(1)牢记“当△≥0时,方程有两个实数根”;(2)牢记两根之和等于-$\frac{b}{a}$、两根之积等于$\frac{c}{a}$.

练习册系列答案
相关题目
7.下列式子的变形中,正确的是( )
| A. | 由6+x=10得x=10+6 | B. | 由2(x-1)=3得2x-1=3 | ||
| C. | 由3x+5=4x得3x-4x=-5 | D. | 由8x=4-3x得8x-3x=4 |
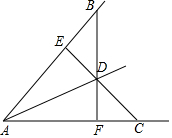 如图,BD=CD,BF⊥AC于F,CE⊥AB于E.求证:点D在∠BAC的角平分线上.
如图,BD=CD,BF⊥AC于F,CE⊥AB于E.求证:点D在∠BAC的角平分线上.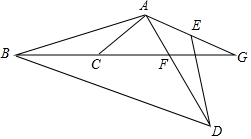 如图所示,AE=AC,AD=AB,∠GAC=∠BAD=110°,∠ACB=130°,求∠G的度数.
如图所示,AE=AC,AD=AB,∠GAC=∠BAD=110°,∠ACB=130°,求∠G的度数.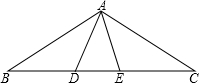 如图,在△ABC中,AD=AE,BD=CE,∠ADB=∠AEC,那么△ABD≌△ACE,△ABE≌ACD..
如图,在△ABC中,AD=AE,BD=CE,∠ADB=∠AEC,那么△ABD≌△ACE,△ABE≌ACD..