题目内容
已知△ABC是半径为2的圆内接三角形,若BC=2
,则∠A的度数为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、60°或120° |
考点:圆周角定理,垂径定理,特殊角的三角函数值
专题:
分析:首先根据题意画出图形,然后由圆周角定理与含30°角的直角三角形的性质,求得答案.
解答:解: 如图,作直径BD,连接CD,则∠BCD=90°,
如图,作直径BD,连接CD,则∠BCD=90°,
∵△ABC是半径为2的圆内接三角形,BC=2
,
∴BD=4,
∴CD=
=2,
∴CD=
BD,
∴∠CBD=30°,
∴∠A=∠D=60°,
∴∠A′=180°-∠A=120°,
∴∠A的度数为:60°或120°.
故选D.
 如图,作直径BD,连接CD,则∠BCD=90°,
如图,作直径BD,连接CD,则∠BCD=90°,∵△ABC是半径为2的圆内接三角形,BC=2
| 3 |
∴BD=4,
∴CD=
| BD2-BC2 |
∴CD=
| 1 |
| 2 |
∴∠CBD=30°,
∴∠A=∠D=60°,
∴∠A′=180°-∠A=120°,
∴∠A的度数为:60°或120°.
故选D.
点评:此题考查了圆周角定理与含30°角的直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
代数式2x-1与3-x的值的符号相同,则x的取值范围是( )
| A、x>3 | ||
B、x<
| ||
C、
| ||
D、x<
|
 如图是测量一颗玻璃球体积的过程:①将300ml的水倒进一个容量为500ml的杯子中;②将四颗相同的玻璃球放入水中,结果水没有满;③再加一颗同样的玻璃球放入水中,结果水满且溢出.根据以上过程,推测这样一颗玻璃球的体积在( )
如图是测量一颗玻璃球体积的过程:①将300ml的水倒进一个容量为500ml的杯子中;②将四颗相同的玻璃球放入水中,结果水没有满;③再加一颗同样的玻璃球放入水中,结果水满且溢出.根据以上过程,推测这样一颗玻璃球的体积在( )| A、20cm3以上,30cm3以下 |
| B、30cm3以上,40cm3以下 |
| C、40cm3以上,50cm3以下 |
| D、50cm3以上,60cm3以下 |
定义一种新运算:观察下列各式:1?3=1×4+3=7,3?1=3×4+1=13,5?4=5×4+4=24,则4?3的值为( )
| A、15 | B、23 | C、16 | D、19 |
 如图,已知∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于点D,AD=2.5cm,DE=1.7cm,则BE=( )
如图,已知∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于点D,AD=2.5cm,DE=1.7cm,则BE=( )| A、1cm | B、0.8cm |
| C、4.2cm | D、1.5cm |
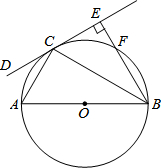 如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,交圆与点F,连接AC、BC.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,交圆与点F,连接AC、BC.