Question

【题目】问题探究题

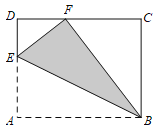
问题背景：如图1，在中，、、三边的长分别为，，，求的面积．

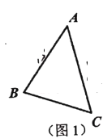
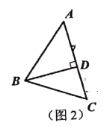
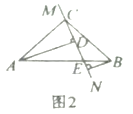
（1）问题解决：小明在计算这个三角形面积的时候，采用了传统的三角形面积计算公式的方法计算，即求出三角形的一条高.如图2，他过点作于点，为了求出高的长，他设，则，根据勾股定理，可列方程：_______________________，该方程解得__________，再根据股定理求出高的长，从而计算的面积（注：此小问不用计算的长和的面积）；

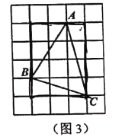
（2）思维拓展：小辉同学在思考这个问题时，觉得小明的方法在计算上比较复杂，他先建立了一个正方形网格（每个正方形网格的边长是1），再在网格中画出了格点（即的三个顶点都在正方形的网格线的交点处），如图3，这样就不用求的高，直接借助网格就能计算的面积为__________（直接写出的面积即可）；

（3）方法应用：我们将小辉的方法称为“构图法”，若的三边长分别为，，（），请在图4的网格中（网格中每个小正方形的边长为）画出相应的，并求出它的面积；

（4）探索创新：若中有两边长为，，且的面积为2，请在图5和备用图的正方形网格中画出所有可能情况（全等三角形视为同一种情况），则的第三边长为______________（直接写出所有可能的情况）．

Answer 1

【答案】（1），；（2）5.5；（3）作图见解析，S△ABC=5；（4）作图见解析，4或．

【解析】

（1）在Rt△ABD中，BD2+AD2=AB2，在Rt△BCD中，BD2+CD2=BC2，由此可得，即可得出方程求解；

（2）利用矩形面积减去三个直角三角形的面积即可得△ABC的面积；

（3）利用，，，即可画出三角形，并按照（2）的方法求面积；

（4）先画出符合条件的图形，再根据勾股定理求出第三边长．

（1）∵在Rt△ABD中，BD2+AD2=AB2，在Rt△BCD中，BD2+CD2=BC2，

∴，

又∵，，，

∴

解得

故答案为：，；

（2）S△ABC=

故答案为：5.5；

（3）如图所示，，，，

S△ABC=

（4）如图所示，符合题意的三角形有2个，△ABC与△ABC'，

其中，AB=，AC=BC'=

∴第三边长BC=4或AC'=

故答案为：4或．