题目内容
13．下列四张扑克牌图案，属于中心对称的是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 根据中心对称图形的概念和各扑克牌的花色排列特点的求解．
解答 解：A、是中心对称图形，符合题意；
B、不是中心对称图形，不符合题意；
C、不是中心对称图形，不符合题意；
D、不是中心对称图形，不符合题意．
故答案为：A．
点评 本题考查中心对称的知识，掌握好中心对称图形的概念是解题的关键．
如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．
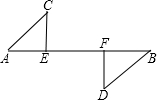如图，CE⊥AB，DF⊥AB，垂足分别为E、F，AC∥DB，且AC=BD，那么Rt△AEC≌Rt△BFD的理由是（ ）
如图，CE⊥AB，DF⊥AB，垂足分别为E、F，AC∥DB，且AC=BD，那么Rt△AEC≌Rt△BFD的理由是（ ）| A． | SSS | B． | AAS | C． | SAS | D． | HL |
4．下列图案中，是轴对称图形且有两条对称轴的是（ ）
| A． |  | B． |  | C． |  | D． |  |
1．
如图所示，能读出的线段条数共有（ ）
如图所示，能读出的线段条数共有（ ）| A． | 8条 | B． | 10条 | C． | 6条 | D． | 12条 |
8．若等腰三角形的周长为28cm，一边为10cm，则腰长为（ ）
| A． | 10cm | B． | 9cm | C． | 10cm或9cm | D． | 8cm |
如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（ ）
5．下列计算结果正确的是（ ）
| A． | -（2x-y）=-2x-y | B． | -3a+（4a2+2）=-3a+4a2-2 | ||
| C． | -（2a-3y）=-2a+3y | D． | -3（a-7）=-3a+7 |
3．用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为0.9，下列说法正确的是（ ）
| A． | 种植10棵幼树，结果一定是“有9棵幼树成活” | |
| B． | 种植100棵幼树，结果一定是“90棵幼树成活”和“10棵幼树不成活” | |
| C． | 种植10n棵幼树，恰好有“n棵幼树不成活” | |
| D． | 种植n棵幼树，当n越来越大时，种植成活幼树的频率会越来越稳定于0.9 |