题目内容
如图，点E、A、C在一条直线上，AD⊥BC，EG⊥BC，垂足分别为D、G，EG与AB相交于点F，且∠1=∠2，∠BAD与∠CAD相等吗？为什么？考点：平行线的判定与性质
专题：
分析：由条件可证明AD∥BG，结合平行线的性质可得∠1=∠CAD，∠2=∠BAD，结合条件可得∠BAD=∠CAD．
解答：解：相等．理由如下：
∵AD⊥BC，EG⊥BC，
∴AD∥EG，
∴∠1=∠CAD，∠2=∠BAD，
∵∠1=∠2，
∴∠BAD=∠CAD．
∵AD⊥BC，EG⊥BC，
∴AD∥EG，
∴∠1=∠CAD，∠2=∠BAD，
∵∠1=∠2，
∴∠BAD=∠CAD．
点评：本题主要考查平行线的判定和性质，掌握平行线的判定和性质是解题的关键，即①同位角相等?两直线平行，②内错角相等?两直线平行，③同旁内角互补?两直线平行．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
如图，三条直线AB，CD，EF相交于一点O，且OF平分∠BOD，那么∠3=∠4吗？为什么？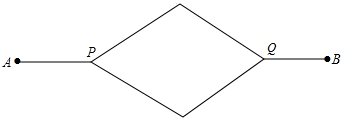
如图所示的道路，自A处出发通过P，Q到达B处，P，Q是三岔路口，假设当来到这些地点处就掷硬币，若出现正面就向右前进，若出现反面就向左前进，现若设掷硬币的次数是在四次以内，求到达B处的概率．
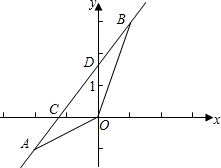如图，已知A（-2，-1），B（1，3）两点在一次函数y=