题目内容
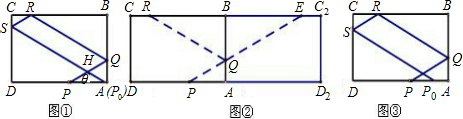
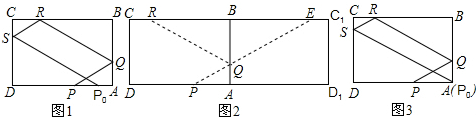
长方形台球桌ABCD上，一球从AB边上某处P击出，分别撞击球桌的边BC、DA各1次后，又回到出发点P处，每次球撞击桌边时，撞击前后的路线与桌边所成的角相等（例如图∠α=∠β）若AB=3，BC=4，则此球所走路线的总长度（不计球的大小）为（ ）分析：要求球走过的总长度，就要求PQ+QR，根据计算得PQ+QR=BD=AC．根据此关系式可以解题．
解答：
解：令PQ∥AC，则QR∥BD，
∵撞击前后的路线与桌边所成的角相等
∴图中所有三角形均相似；
∴
=
，
=
，
∴
+
=
=1，
即PQ+QR=AC=BD，
同理PS+SR=AC=BD，
∴PQ+QR+RS+SP=AC+BD=2AC．
∵AC=
=5，
∴PQ+QR+RS+SP=AC+BD=2AC=10．
故选 D．
解：令PQ∥AC，则QR∥BD，∵撞击前后的路线与桌边所成的角相等
∴图中所有三角形均相似；
∴
| PQ |
| AC |
| BQ |
| BC |
| QR |
| BD |
| CQ |
| BC |
∴
| PQ |
| AC |
| QR |
| BD |
| BC |
| BC |
即PQ+QR=AC=BD，
同理PS+SR=AC=BD，
∴PQ+QR+RS+SP=AC+BD=2AC．
∵AC=
| 32+42 |
∴PQ+QR+RS+SP=AC+BD=2AC=10．
故选 D．
点评：本题考查了直角三角形中勾股定理的运用，考查了相似三角形对应边比例相等的性质，本题中令PQ∥AC是解题的关键．
练习册系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
