题目内容
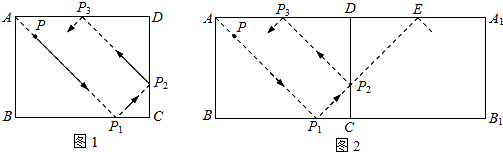
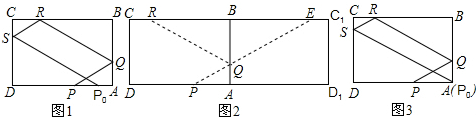
小冬遇到一个有趣的问题:长方形台球桌ABCD的边长分别为AB=3,BC=5.点P在AD上,且AP=2.一球从点P处沿与AD夹角为θ的方向击出,分别撞击AB、BC、CD各一次后到达点P0.每次撞击桌边时,撞击前后的路线与桌边所成的角相等(入射角等于反射角).如图①所示.小冬的思考是这样开始的:如图②,将矩形ABCD沿直线AB折叠,得到矩形ABC1D1,由轴对称的知识,发现QE=QR,PE=PQ+QR.请你参考小冬的思路或想出自己的方法解决下列问题:
(1)点P0与点A重合时,此球所经过的路线总长度是
(2)当点P0落在线段AP上时(如图③),求tanθ的取值范围.
分析:(1)根据题意得到∠HQA=∠HAQ,∠HPA=∠HAP,推出△RCS∽△PAQ,得出比例式,求出CR,根据勾股定理求出PE即可.
(2)由(1)得出tanθ=
,即可得出答案.
(2)由(1)得出tanθ=
| 1 |
| 2 |
解答: 解:(1)AS交PQ于H,
解:(1)AS交PQ于H,
根据入射角等于反射角得到∠HQA=∠HAQ,∠HPA=∠HAP,
∴PQ=2HP=2HQ=2SR,
∵∠C=∠A=90°,∠CRS=∠QPA,
∴△RCS∽△PAQ,
∴
=
=2,
∵PA=2,
∴CR=1,
EC2=1,
由勾股定理得:PE=
=3
,
同理:SR+AS=
=3
,
∴3
+3
=6
,
故答案为:6
.
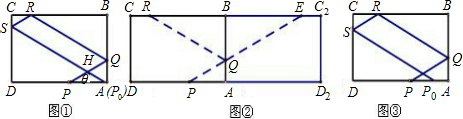
(2)由(1)知:BR=5-1=4,
∴
=
=
,
∵AB=3,
∴AQ=1,
∴tanθ=
=
,
当P0在P点上时,tanθ=
,
∴当点P0落在线段AP上时,tanθ的取值范围是
≤tanθ≤
.
 解:(1)AS交PQ于H,
解:(1)AS交PQ于H,根据入射角等于反射角得到∠HQA=∠HAQ,∠HPA=∠HAP,
∴PQ=2HP=2HQ=2SR,
∵∠C=∠A=90°,∠CRS=∠QPA,
∴△RCS∽△PAQ,
∴
| AP |
| CR |
| PQ |
| SR |
∵PA=2,
∴CR=1,
EC2=1,
由勾股定理得:PE=
| (2-1+5)2+32 |
| 5 |
同理:SR+AS=
| (5+1)2+32 |
| 5 |
∴3
| 5 |
| 5 |
| 5 |
故答案为:6
| 5 |
(2)由(1)知:BR=5-1=4,
∴
| AQ |
| BQ |
| AP |
| BR |
| 1 |
| 2 |
∵AB=3,
∴AQ=1,
∴tanθ=
| AQ |
| AP |
| 1 |
| 2 |
当P0在P点上时,tanθ=
| 3 |
| 5 |
∴当点P0落在线段AP上时,tanθ的取值范围是
| 1 |
| 2 |
| 3 |
| 5 |
点评:本题主要考查对勾股定理,矩形的性质,轴对称性质,解直角三角形,翻折变换等知识点的理解和掌握,能综合运用性质进行推理是解此题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目