题目内容
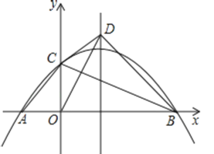
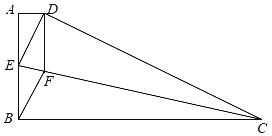
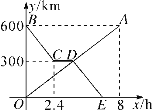
【题目】货车和轿车分别从甲、乙两地同时出发，沿同一公路相向而行．轿车出发2.4h后休息，直至与货车相遇后，以原速度继续行驶．设货车出发xh后，货车、轿车分别到达离甲地y1km和y2km的地方，图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系．
(1)求点D的坐标，并解释点D的实际意义；
(2)求线段DE所在直线的函数表达式；
(3)当货车出发________h时，两车相距200km．
【答案】(1) (4，300)，货车出发4h后，与轿车在距离A地300km处相遇； (2) y＝-125x+800； (3) 2或5
【解析】
（1）待定系数法求出
的解析式，再根据点
的纵坐标为300求得其横坐标，即可得解；
（2）轿车在休息前
行驶
，休息后按原速度行驶，可得轿车行驶后需，从而可得点
的坐标，再结合点的坐标，用待定系数法可求得答案；
（3）先用待定系数法求出
段的解析式，然后分两种情况列方程求解即可：①当轿车休息前与货车相距200km时；②当轿车休息后与货车相距200km时．
解：(1)设OA所在直线解析式为y＝mx，
将A(8，600)代入，得600＝8m，解得m＝75，
∴OA所在直线的解析式为y＝75x．
令y＝300，得75x＝300，解得x＝4，
∴点D坐标为(4，300)，其实际意义为货车出发4h后，与轿车在距离A地300km处相遇．
故答案为：点D坐标为(4，300)，其实际意义为货车出发4h后，与轿车在距离A地300km处相遇．
(2)由图象知，轿车在休息前2.4h行驶距离为300km，
休息后按原速度行驶，
∴轿车行驶后需，
又因为点坐标为
，
故点E坐标为(6.4，0)，
设线段
所在直线的函数表达式为
将点
，
代入得：
解得
线段所在直线的函数表达式为
；
(3)2或5
设段的函数解析式为
将
，
代入得：
解得：
①当轿车休息前与货车相距200km时，有-125x+600-75x＝200，解得x＝2；
②当轿车休息后与货车相距200km时，有75x-(-125x+800)＝200，解得x＝5．
故答案为：2或5．
