题目内容
9.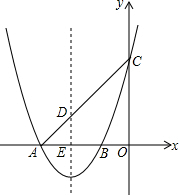 如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C,
如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C,(1)求抛物线的对称轴及点A的坐标;
(2)在平面直角坐标系xOy中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由.
分析 (1)根据二次函数y=ax2+bx+c的对称轴为x=-$\frac{b}{2a}$,求得抛物线的对称轴,因为函数与X轴的交点是y=0,列方程即可求得;
(2)分别以AC,AB为对角线各可求得一点,再以AC,AB为边求得一点.
解答 解:(1)①对称轴x=-$\frac{4}{2}$=-2;
②当y=0时,有x2+4x+3=0,
解得x1=-1,x2=-3,
故点A的坐标为(-3,0).
(2)如图所示,满足条件的点P有3个,分别为(-2,3),(2,3),(-4,-3).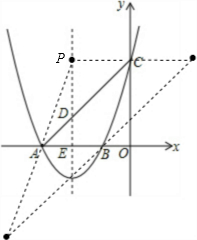
点评 此题考查了二次函数综合题,涉及二次函数与一次函数,四边形的综合知识,解题的关键是要注意数形结合思想的应用.此题属于中考中的压轴题,难度较大,知识点考查的较多而且联系密切,需要学生认真审题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.两圆的圆心都是O,半径分别为r1,r2(r1<r2),若r1<OP<r2,则点P在( )
| A. | 大圆外 | B. | 小圆内 | C. | 大圆内,小圆外 | D. | 无法确定 |
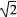 +b+3=0,其中a、b为有理数,那么a=______________;
+b+3=0,其中a、b为有理数,那么a=______________;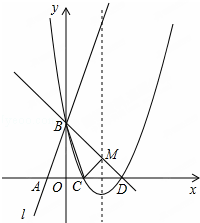 如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).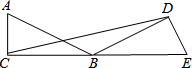 如图,把一个直角三角形ACB绕着30°角的顶点B顺时针旋转,使点A与CB的延长线上的点E重合,这时旋转角的度数是150°.
如图,把一个直角三角形ACB绕着30°角的顶点B顺时针旋转,使点A与CB的延长线上的点E重合,这时旋转角的度数是150°.