题目内容
11. 如图,N为x轴负半轴上一点,MB∥NO,OD平分∠AON,延长AB交OD于C,BC平分∠DBM,且∠D+$\frac{1}{2}$∠A=60°,求∠DBM的度数.
如图,N为x轴负半轴上一点,MB∥NO,OD平分∠AON,延长AB交OD于C,BC平分∠DBM,且∠D+$\frac{1}{2}$∠A=60°,求∠DBM的度数.
分析 根据角平分线的定义和平行线的性质∠1=∠2=∠3=∠4+∠6,再根据外角的性质和角平分线的定义得出∠2=∠3=∠D+∠DBM,再根据三角形的内角和定理得出∠DBM.
解答 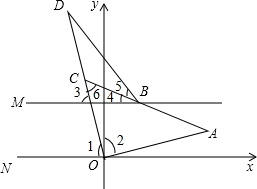 解:∵OD平分∠AON,
解:∵OD平分∠AON,
∴∠1=∠2,
∵AN∥BM,
∴∠1=∠2=∠3=∠4+∠6,
又BC平分∠DBM,∠6=∠D+∠5,
∴∠4=∠5=$\frac{1}{2}$∠DBM,∠6=∠D+$\frac{1}{2}$∠DBM,
∴∠2=∠3=$\frac{1}{2}$∠DBM+(∠D+$\frac{1}{2}$∠DBM)=∠D+∠DBM,
在△AOC中,∠2+∠6+∠A=180°,
即(∠D+∠DBM)+(∠D+$\frac{1}{2}$∠DBM)+∠A=(2∠D+∠A)+$\frac{3}{2}$∠DBM=180°,
∵∠D+$\frac{1}{2}$∠A=60°,
∴2∠D+∠A=120°,
∴∠DBM=$\frac{2}{3}$(180°-120°)=40°.
点评 本题考查了平行线的性质以及三角形的内角和定理,把未知转化成已知,在同一个三角形中利用三角形的内角和等于180求解是解题的关键.

练习册系列答案
相关题目
19.某学校为了了解学生做课外作业所用时间的情况,对学生做课外作业所用时间进行调查,下表是该校八年级某班50名学生某一天做数学课外作业所用时间情况的统计表:
该班学生做数学课外作业所用时间的中位数落在哪个时间段内?
| 所用时间t/min | 人数 |
| 0<t≤10 | 4 |
| 10<t≤20 | 6 |
| 20<t≤30 | 14 |
| 30<t≤40 | 13 |
| 40<t≤50 | 9 |
| 50<t≤60 | 4 |
20.两圆的圆心距为8,两圆的半径为2和5,则这两个圆的位置关系是( )
| A. | 相交 | B. | 外离 | C. | 内切 | D. | 外切 |

 如图,在平面直角坐标系中,直线y=x+4与抛物线y=ax2-3x+c交于A、B两点,点A在x轴上,点B在y轴上.
如图,在平面直角坐标系中,直线y=x+4与抛物线y=ax2-3x+c交于A、B两点,点A在x轴上,点B在y轴上. 平面上有△ACD与△BCE,其中AD与BE相交于P点,若AC=BC,CD=CE,∠ACB=∠ECD.
平面上有△ACD与△BCE,其中AD与BE相交于P点,若AC=BC,CD=CE,∠ACB=∠ECD.